랜덤 넘버는 암호학에서 자주 쓰인다.
- nonces는 한 번만 사용되는 일회용 값으로, 재생공격을 방지하는데 사용된다.
- 세션 키는 각 세션마다 랜덤으로 생성된다.
- 공개 키 생성에서 키 쌍을 생성할 때 랜덤으로 생성된다.
랜덤 넘버는 통계학적으로 무작위여야하고, 각 난수는 서로 독립적이고 예측 불가능해야한다.
TRNG
실제 무작위 소스를 랜덤생성기의 입력으로 사용한다.
무작위 소스는 엔트로피 소스라고 부른다. 컴퓨터의 물리적 환경에서 얻을 수 있다.
예를 들어, 키보드 - 마우스 타이핑 패턴 및 속도, 디스크의 전기적 활동, 시스템 클럭의 순간 값과 환경 소음이나 온도 변동 등 물리적인, 아날로그 소스 값을 이진 출력으로 변환하여 사용한다.
PRNG
Pseudorandom Number Generator, 결정론적 알고리즘으로 동일한 입력에 대해 항상 동일한 출력을 내놓는다.
완전한 무작위가 아니지만 여러 랜덤성 테스트를 통과한다.
- Randomness : 균일 분포와 다양한 크기와 범위를 효율적으로 나타내고 일관된 방식으로 랜덤 넘버를 반환한다.
- Unpredictability : 시드값을 모르면 하나의 난수로부터 이전과 이후 값을 예측이 어렵고, 시드값 역추적도 어려워야한다.
- Use same tests to check : 생성기가 사용하는 시드의 특성을 검사하기 위해 동일한 랜덤성 테스트를 사용해야한다.
- Secure : 시드값은 랜덤이고 안전해야한다. 따라서 시드를 결정할 때 TRNG로 생성한다.
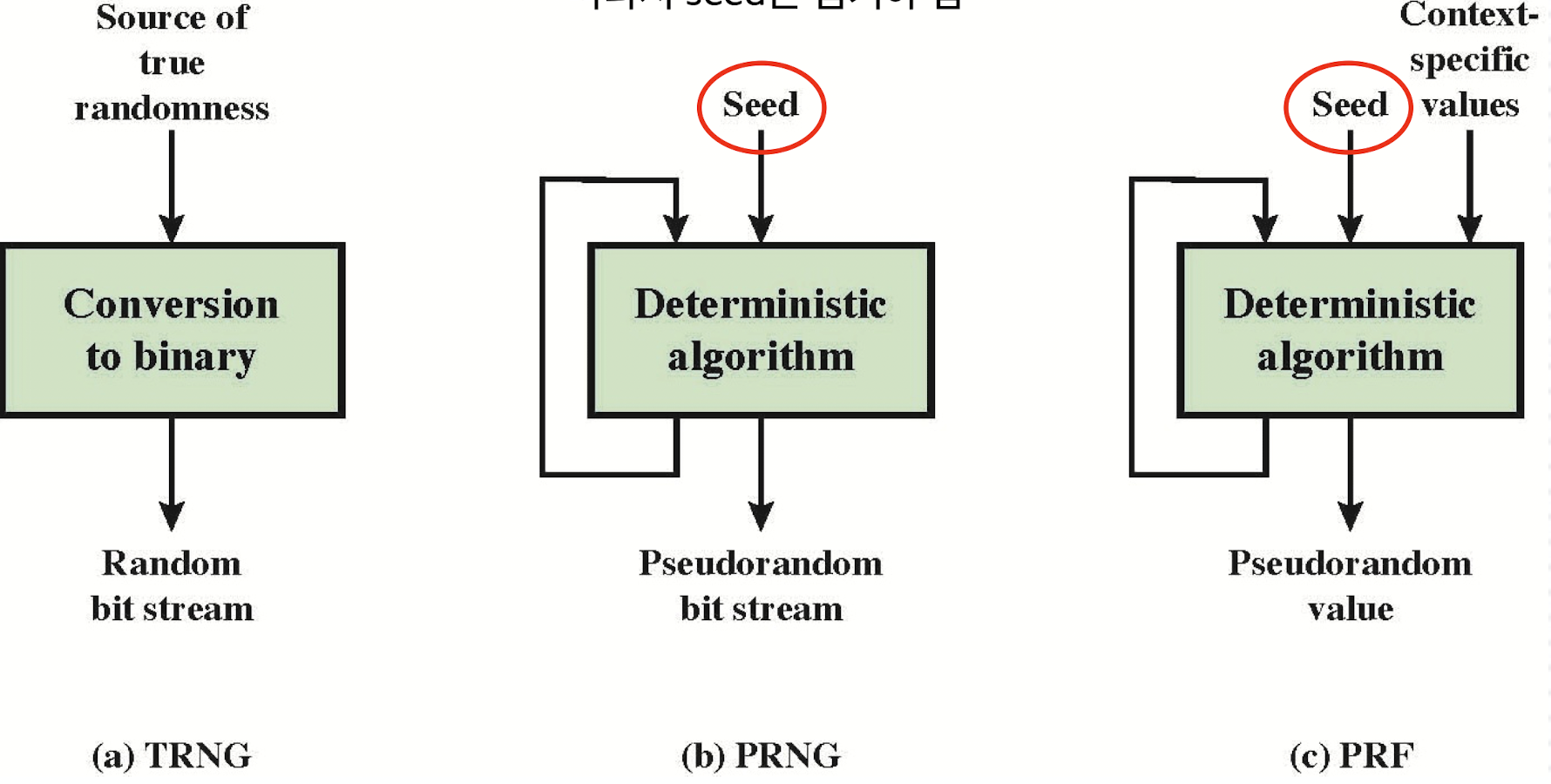
여기서 PRF(Pseudorandom Function)는 시드뿐만 아닌 다른 값도 입력으로 받을 수 있다.
Linear Congruential Generator (LCG)
x_(n+1) = (a * x_n + c) mod m
간단한 랜덤 넘버 생성기이다. 어떤 값 a,c,m에 대해 이전 값 x_n으로부터 다음 값을 얻는다.
일부 숫자 획득하면 시퀀스 재구성이 가능하기에 암호학에선 사용되지 않는다.
Blum Blum Shub Generator
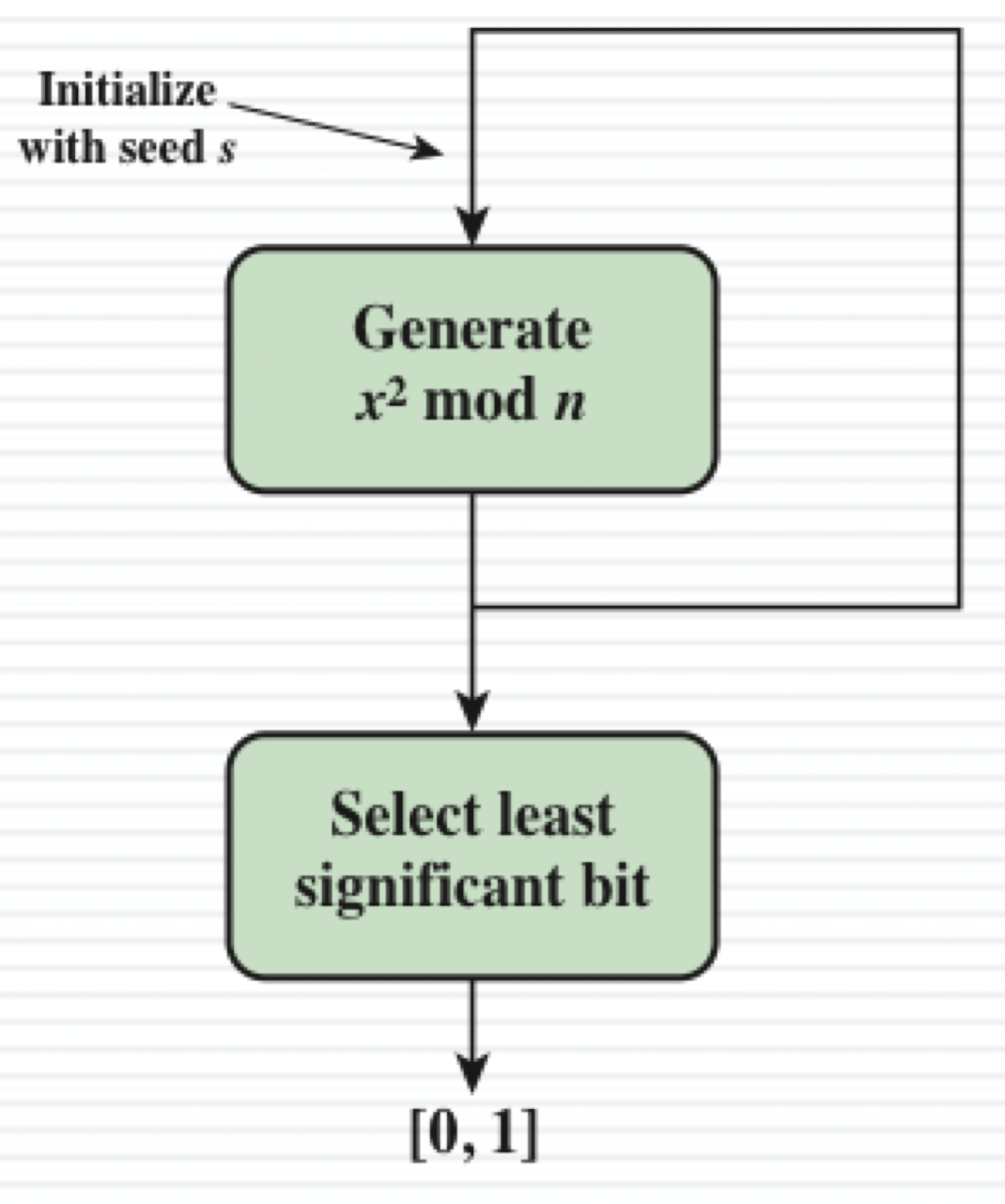
공개키 알고리즘을 기반으로 한다.
x_i = x_(i-1)^2 mod n 에서 최하위 비트를 사용하며, n=pq로 p와 q는 mod 4가 3인 소수이다.
보안성은 n을 인수분해하는 어려움에 기반한다.
매우 큰 숫자를 사용하기에 속도가 느려서 암호화 사용에 적합하지 않지만 키 생성에는 적합하다.
ANSI X9.17 PRG
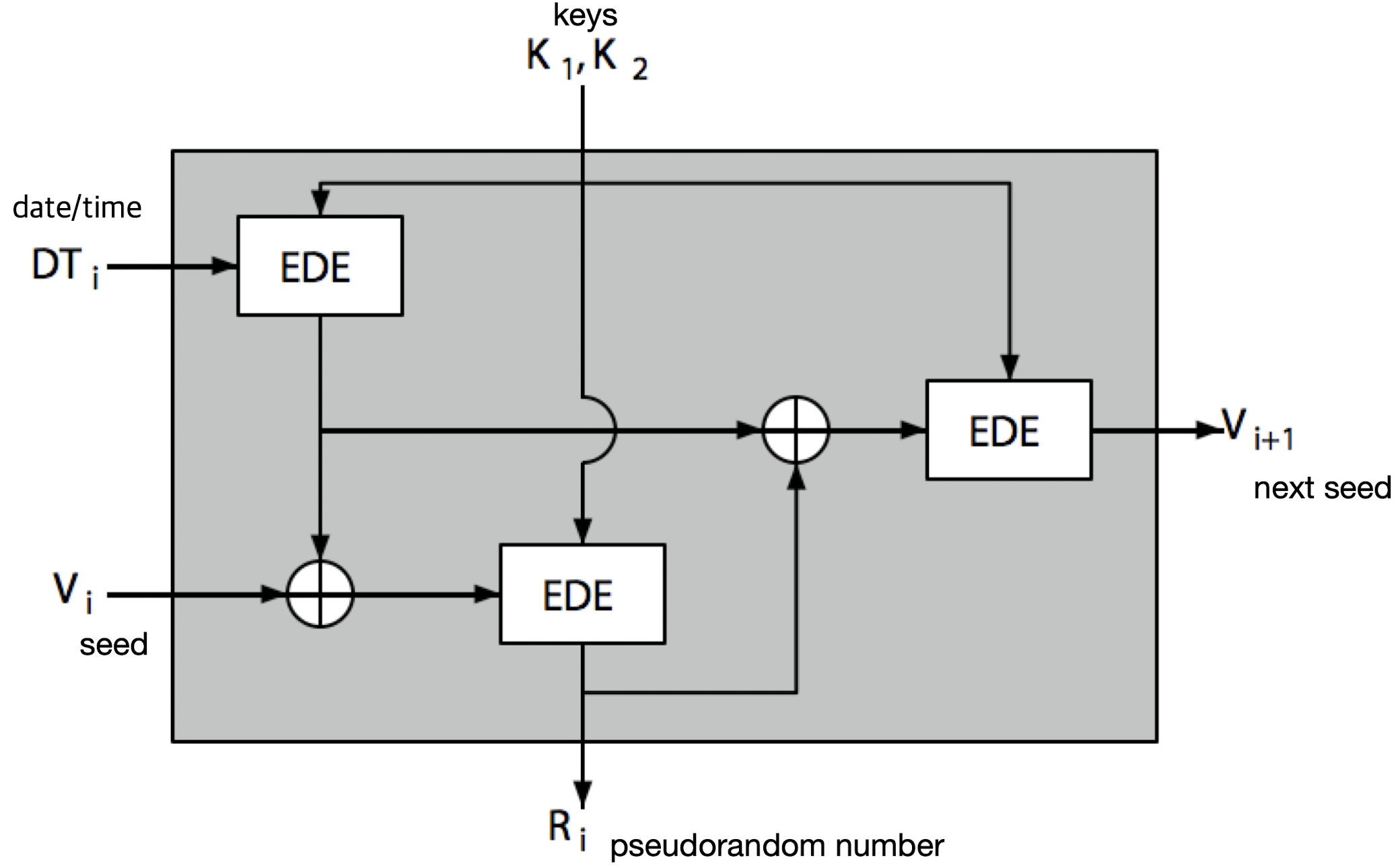
block 암호화 알고리즘으로 랜덤 생성한다. block 암호화 알고리즘으로 생성된 키가 랜덤하다는 것을 보여준다.
EDE는 3 DES with K1 and K2 이다.
CTR_DRBG
CTR_DRBG는 카운터 모드를 사용해서 랜덤 비트를 생성한다. 블록 암호를 사용하여 카운터 값을 암호화하고 그 결과를 랜덤 비트 시퀀스로 사용하는 방식이다.
시드 길이는 키 길이와 출력 블록 길이의 합과 같다.
생성기가 reseed_interval만큼의 랜덤 넘버를 생성하고 나면 새로운 시드값으로 재설정한다.
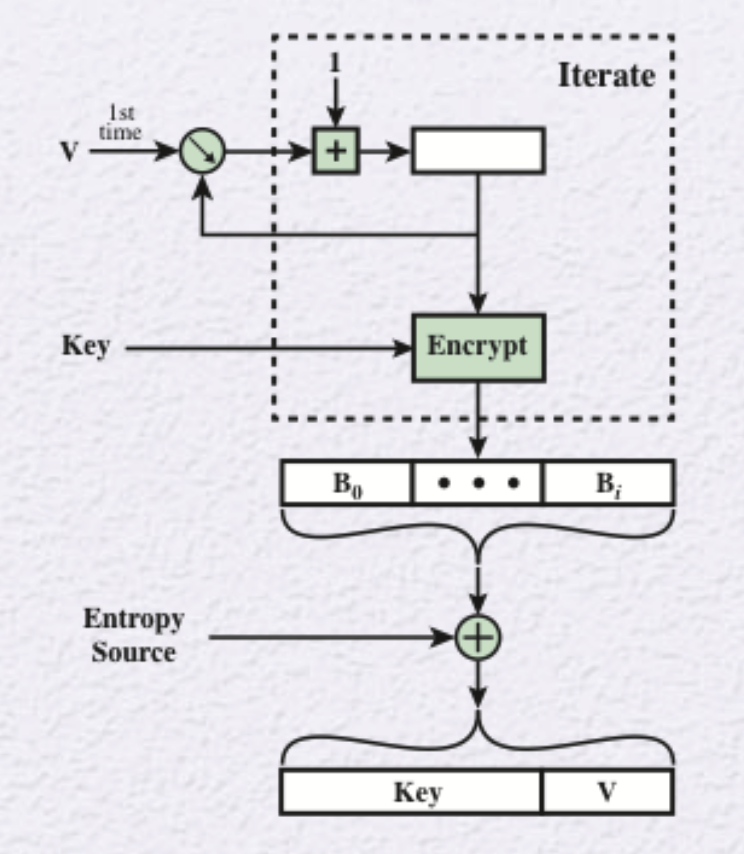
어느 값 v에 key에 대하여, 출력값의 총 길이가 시드의 길이가 될 때까지 점선 박스 내부의 과정을 반복한다. 카운터모드이기에 매 반복마다 v값에 1을 더한다.
그렇게 얻은 값에 엔트로피 소스를 연산하여 시드를 생성한다.
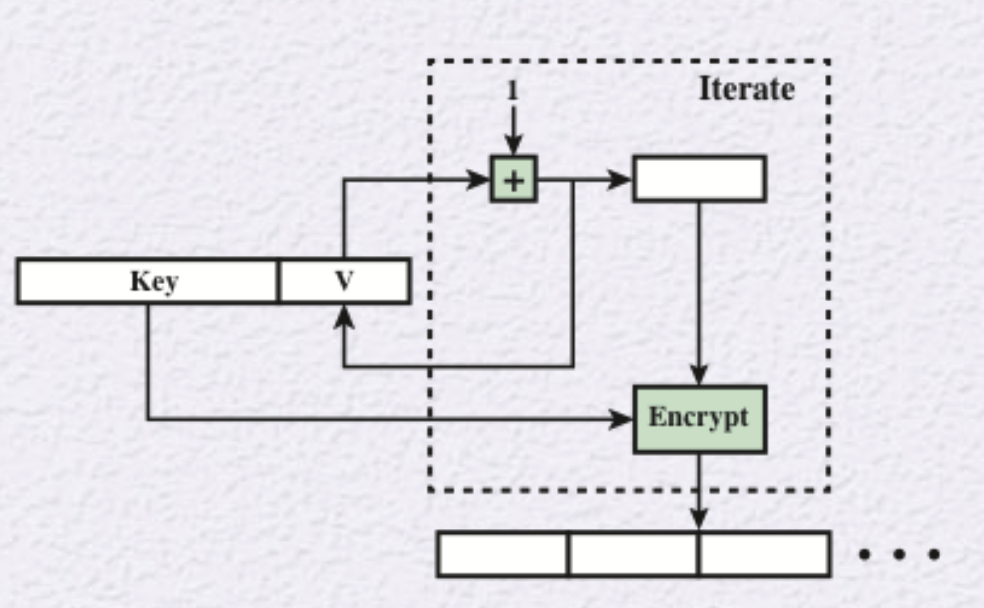
시드는 key와 v로 구성돼있다. key로 v를 암호화하는 방식으로 랜덤 넘버를 생성한다. 매 생성마다 v에는 1을 더해준다.
Stream Cipher Structure

단순하게 어떤 값 M에 대해 key를 랜덤생성하여 XOR 연산하며 랜덤 넘버를 생성한다.
장점은 빠르며, 랜덤 반복의 주기가 길다. 단, 키를 중복 사용해선 안되기에 매번 키를 생성해야한다.
RC4
RC4는 설계가 단순하고, 효과적인 알고리즘이였다.
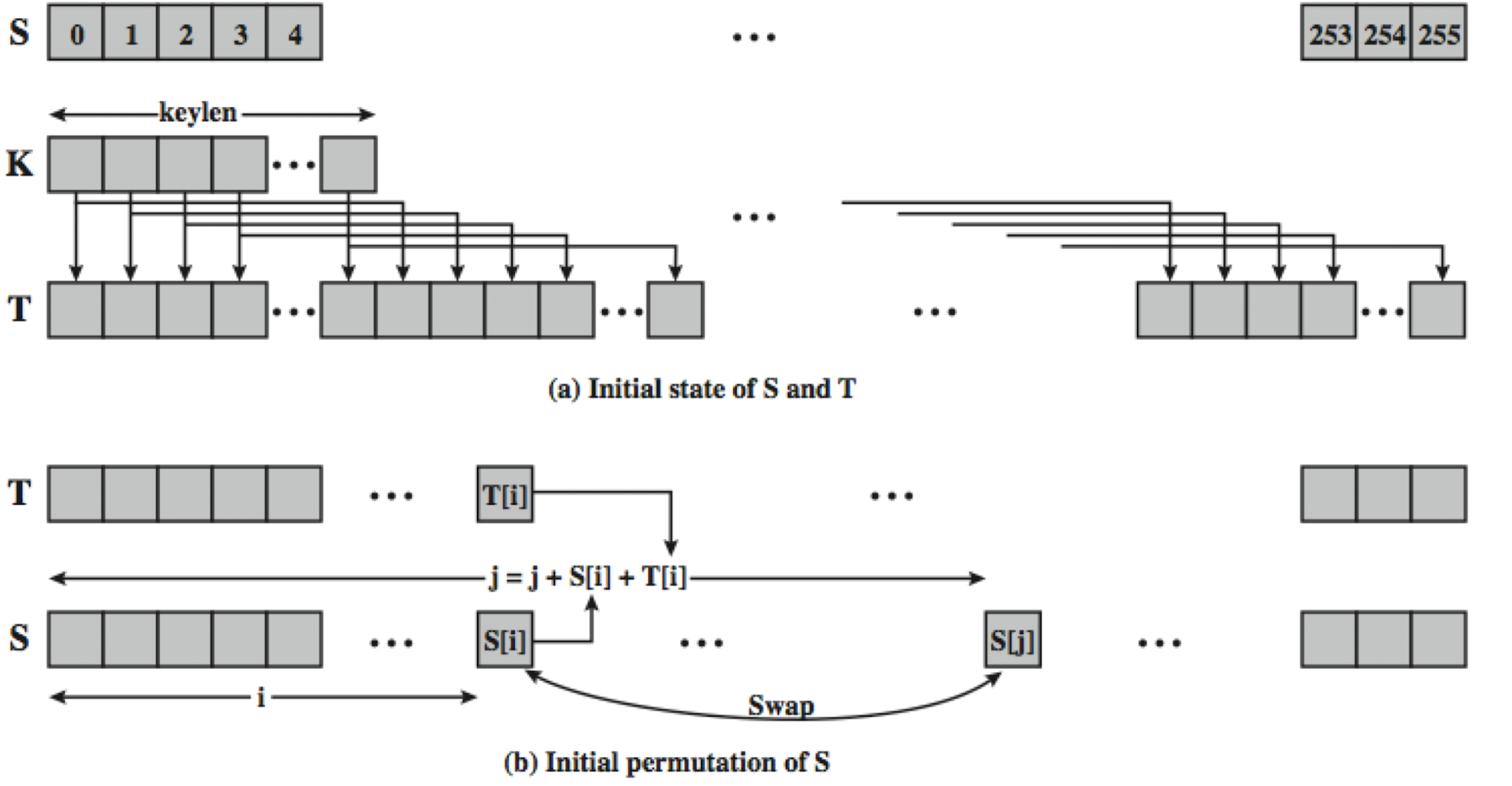
먼저 랜덤 생성을 위한 초기값으로, 0~255까지 있는 S와 keylen 길이의 K를 준비한다.
T는 K가 S의 길이만큼 순차적으로 반복하여 들어가있는 배열이다.
S 배열을 i=0에서부터 끝까지 j와 스왑한다. 여기서 초기에 0으로 초기화돼있던 j는 j + S[i] + T[i]이다.

랜덤을 생성할 때는 초기값 i=0, j=0에 대하여,
i = (i+1) mod 256, j = (j+S[i]) mod 256 이다.
S[i]와 S[j]의 위치를 바꾸고, t = (S[i] + S[j]) mod 256 이다.
평문 (여기서는 시드) M_i와 S[t]와 XOR연산을 한다.
지금은 매우 안전하지 않아서 사용되지 않는다.
'학교강의필기장 > 암호학' 카테고리의 다른 글
| 7. public key system (0) | 2023.10.18 |
|---|---|
| 6. number theory (1) | 2023.10.17 |
| 4. DES, block/stream cipher mode (0) | 2023.10.15 |
| 3. AES (0) | 2023.10.12 |
| 2. 모듈러 연산 (1) | 2023.10.10 |
랜덤 넘버는 암호학에서 자주 쓰인다.
- nonces는 한 번만 사용되는 일회용 값으로, 재생공격을 방지하는데 사용된다.
- 세션 키는 각 세션마다 랜덤으로 생성된다.
- 공개 키 생성에서 키 쌍을 생성할 때 랜덤으로 생성된다.
랜덤 넘버는 통계학적으로 무작위여야하고, 각 난수는 서로 독립적이고 예측 불가능해야한다.
TRNG
실제 무작위 소스를 랜덤생성기의 입력으로 사용한다.
무작위 소스는 엔트로피 소스라고 부른다. 컴퓨터의 물리적 환경에서 얻을 수 있다.
예를 들어, 키보드 - 마우스 타이핑 패턴 및 속도, 디스크의 전기적 활동, 시스템 클럭의 순간 값과 환경 소음이나 온도 변동 등 물리적인, 아날로그 소스 값을 이진 출력으로 변환하여 사용한다.
PRNG
Pseudorandom Number Generator, 결정론적 알고리즘으로 동일한 입력에 대해 항상 동일한 출력을 내놓는다.
완전한 무작위가 아니지만 여러 랜덤성 테스트를 통과한다.
- Randomness : 균일 분포와 다양한 크기와 범위를 효율적으로 나타내고 일관된 방식으로 랜덤 넘버를 반환한다.
- Unpredictability : 시드값을 모르면 하나의 난수로부터 이전과 이후 값을 예측이 어렵고, 시드값 역추적도 어려워야한다.
- Use same tests to check : 생성기가 사용하는 시드의 특성을 검사하기 위해 동일한 랜덤성 테스트를 사용해야한다.
- Secure : 시드값은 랜덤이고 안전해야한다. 따라서 시드를 결정할 때 TRNG로 생성한다.

여기서 PRF(Pseudorandom Function)는 시드뿐만 아닌 다른 값도 입력으로 받을 수 있다.
Linear Congruential Generator (LCG)
x_(n+1) = (a * x_n + c) mod m
간단한 랜덤 넘버 생성기이다. 어떤 값 a,c,m에 대해 이전 값 x_n으로부터 다음 값을 얻는다.
일부 숫자 획득하면 시퀀스 재구성이 가능하기에 암호학에선 사용되지 않는다.
Blum Blum Shub Generator

공개키 알고리즘을 기반으로 한다.
x_i = x_(i-1)^2 mod n 에서 최하위 비트를 사용하며, n=pq로 p와 q는 mod 4가 3인 소수이다.
보안성은 n을 인수분해하는 어려움에 기반한다.
매우 큰 숫자를 사용하기에 속도가 느려서 암호화 사용에 적합하지 않지만 키 생성에는 적합하다.
ANSI X9.17 PRG

block 암호화 알고리즘으로 랜덤 생성한다. block 암호화 알고리즘으로 생성된 키가 랜덤하다는 것을 보여준다.
EDE는 3 DES with K1 and K2 이다.
CTR_DRBG
CTR_DRBG는 카운터 모드를 사용해서 랜덤 비트를 생성한다. 블록 암호를 사용하여 카운터 값을 암호화하고 그 결과를 랜덤 비트 시퀀스로 사용하는 방식이다.
시드 길이는 키 길이와 출력 블록 길이의 합과 같다.
생성기가 reseed_interval만큼의 랜덤 넘버를 생성하고 나면 새로운 시드값으로 재설정한다.

어느 값 v에 key에 대하여, 출력값의 총 길이가 시드의 길이가 될 때까지 점선 박스 내부의 과정을 반복한다. 카운터모드이기에 매 반복마다 v값에 1을 더한다.
그렇게 얻은 값에 엔트로피 소스를 연산하여 시드를 생성한다.

시드는 key와 v로 구성돼있다. key로 v를 암호화하는 방식으로 랜덤 넘버를 생성한다. 매 생성마다 v에는 1을 더해준다.
Stream Cipher Structure

단순하게 어떤 값 M에 대해 key를 랜덤생성하여 XOR 연산하며 랜덤 넘버를 생성한다.
장점은 빠르며, 랜덤 반복의 주기가 길다. 단, 키를 중복 사용해선 안되기에 매번 키를 생성해야한다.
RC4
RC4는 설계가 단순하고, 효과적인 알고리즘이였다.

먼저 랜덤 생성을 위한 초기값으로, 0~255까지 있는 S와 keylen 길이의 K를 준비한다.
T는 K가 S의 길이만큼 순차적으로 반복하여 들어가있는 배열이다.
S 배열을 i=0에서부터 끝까지 j와 스왑한다. 여기서 초기에 0으로 초기화돼있던 j는 j + S[i] + T[i]이다.

랜덤을 생성할 때는 초기값 i=0, j=0에 대하여,
i = (i+1) mod 256, j = (j+S[i]) mod 256 이다.
S[i]와 S[j]의 위치를 바꾸고, t = (S[i] + S[j]) mod 256 이다.
평문 (여기서는 시드) M_i와 S[t]와 XOR연산을 한다.
지금은 매우 안전하지 않아서 사용되지 않는다.
'학교강의필기장 > 암호학' 카테고리의 다른 글
| 7. public key system (0) | 2023.10.18 |
|---|---|
| 6. number theory (1) | 2023.10.17 |
| 4. DES, block/stream cipher mode (0) | 2023.10.15 |
| 3. AES (0) | 2023.10.12 |
| 2. 모듈러 연산 (1) | 2023.10.10 |
