AES는 DES(Data Encryption Standard)의 취약성을 해결하기 위해 탄생하였다.
Triple DES로 보안을 강화할 수 있었지만, 느리고 블록 크기가 작아서 사용에 제약이 있었다.
그렇게 채택된 암호화 표준인 라인달(Rijndael) 알고리즘이 AES가 되었다.
라인달 암호는 128/192/256 bit key와 128 bit data block을 사용한다.
라인달 암호는 Feistel 구조(데이터 블록을 두 부분으로 나누고 한 부분만 암호화) 대신 반복형 암호를 사용하며 4*4 바이트 블록을 여러 라운드에 걸쳐 처리한다.각 라운드에 전체 데이터 블록에 연산을 적용한다.
AES는 4가지 연산으로 이뤄진다.
1. SubBytes : 각 바이트를 S-box라는 미리 정의된 테이블을 사용해 치환한다.
2. ShiftRows: 블록의 각 행을 다른 양으로 순환 시프트한다.
3. MixColumns: 블록의 각 열을 선형 변환한다.
4. AddRoundKey: 라운드 키를 현재 블록에 XOR연산으로 더한다.
각 연산 방법 세부 사항에 대해 알아보자. 아래 내용은 AES-128을 기반으로 한다.
그 전에, 예제 코드에서 다루는 4*4 바이트 블록의 인덱싱 순서는 다음과 같다.
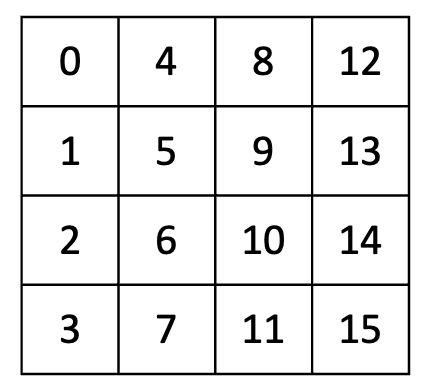
SubBytes
SubBytes는 현재 상태의 각 바이트를 S-box라는 미리 정의된 테이블을 사용해 치환한다. 복호화를 위해서 Inverse S-box도 필요하다.
구현은 간단하게, 4*4로 이뤄진 현재 상태에 모드에 따라 sbox로 치환하거나 isbox로 치환한다.
sbox와 isbox의 값은 https://en.wikipedia.org/wiki/Rijndael_S-box를 참조하자.
sbox = {...};
isbox = {...};
...
void SubBytes(uint8_t *state, int mode)
{
for (int i = 0; i < 16; i++)
{
state[i] = (mode == ENCRYPT) ? sbox[state[i]] : isbox[state[i]];
}
}
ShiftRows
블록의 각 행을 다른 양으로 순환 시프트한다. 첫 번째 행은 시프트하지 않고, 두 번째 행은 1만큼 왼쪽으로 시프트, 세 번째 행은 2, 네 번째 행은 3만큼 왼쪽으로 시프트한다. 복호화 할 때는 반대 방향으로 시프트 한다.
void ShiftRows(uint8_t *state, int mode)
{
uint8_t temp;
if (mode == ENCRYPT)
{
temp = state[1]; state[1] = state[5]; state[5] = state[9];
state[9] = state[13]; state[13] = temp;
temp = state[2]; state[2] = state[10]; state[10] = temp;
temp = state[6]; state[6] = state[14]; state[14] = temp;
temp = state[3]; state[3] = state[15]; state[15] = state[11];
state[11] = state[7]; state[7] = temp;
}
else
{
temp = state[1]; state[1] = state[13]; state[13] = state[9];
state[9] = state[5]; state[5] = temp;
temp = state[2]; state[2] = state[10]; state[10] = temp;
temp = state[6]; state[6] = state[14]; state[14] = temp;
temp = state[3]; state[3] = state[7]; state[7] = state[11];
state[11] = state[15]; state[15] = temp;
}
}
MixColumns
블록의 각 열을 선형 변환한다. 먼저 암호화를 할 때는 다음 행렬과 GF(2^8)에서 행렬곱을 수행한다.
[2 3 1 1]
[1 2 3 1]
[1 1 2 3]
[3 1 1 2]여기서 2로 곱하는 것은 왼쪽 비트시프트를 1만큼 수행하고, 오버플로우 발생 시 불가역다항식과 XOR연산을 한다.
3으로 곱하는 것은 2로 곱한 결과에 원래 값과 XOR연산을 한다.
AES에서 불가역다항식은 x^8 + x^4 + x^3 + x + 1 이다. 이를 GF(2^8)에서 나타내면 00011011(2) = 1b(16)이다.
따라서 2로 곱하는 것은 (((a) << 1) ^ (((a >> 7) & 1) * 0x1b)) 로 나타낼 수 있다.
복호화를 할 때는 위 행렬의 GF(2^8)에서의 역행렬을 사용한다.
[14 11 13 9]
[ 9 14 11 13]
[13 9 14 11]
[11 13 9 14]다음 행렬을 사용하게 되는데, 9,11,13,14의 곱을 수행해야 한다. 곱해야 하는 값을 a라고 할 때,
9a = 2*2*2*a + a
11a = 2*2*2*a + a + 2*a
13a = 2*2*2*a + a + 2*2*a
14 a = 2*2*2*a + 2*a + 2*2*a
로 나타낼 수 있다. 따라서 암호화에서 사용했던 연산 방법을 그대로 사용하여 연산할 수 있다.
아래 코드에서 사용한 M, IM은 행렬곱을 편리하게 하기 위해 전치행렬로 나타낸 상태이다.
#define XTIME(a) (((a) << 1) ^ (((a >> 7) & 1) * 0x1b))
...
uint8_t M[16] = {2, 3, 1, 1, 1, 2, 3, 1, 1, 1, 2, 3, 3, 1, 1, 2};
uint8_t IM[16] = {0x0e, 0x0b, 0x0d, 0x09, 0x09, 0x0e, 0x0b, 0x0d, 0x0d, 0x09, 0x0e, 0x0b, 0x0b, 0x0d, 0x09, 0x0e};
...
void MixColumns(uint8_t *state, int mode)
{
uint8_t temp[16] = {};
for (uint8_t i = 0; i < BLOCKLEN; ++i)
{
uint8_t x = i / Nb, y = i % Nb;
for (int k = y * 4; k < y * 4 + 4; ++k)
{
uint8_t mul = (mode == ENCRYPT ? M[k] : IM[k]);
if (mul == 1)
{
temp[x * 4 + y] ^= state[x * 4 + k % 4];
}
else if (mul <= 3)
{
temp[x * 4 + y] ^= XTIME(state[x * 4 + k % 4]);
if (mul == 3)
{
temp[x * 4 + y] ^= state[x * 4 + k % 4];
}
}
else
{
temp[x * 4 + y] ^= XTIME(XTIME(XTIME(state[x * 4 + k % 4])));
if (mul == 9 || mul == 11 || mul == 13)
{
temp[x * 4 + y] ^= state[x * 4 + k % 4];
}
if (mul == 11 || mul == 14)
{
temp[x * 4 + y] ^= XTIME(state[x * 4 + k % 4]);
}
if (mul == 13 || mul == 14)
{
temp[x * 4 + y] ^= XTIME(XTIME(state[x * 4 + k % 4]));
}
}
}
}
for (uint8_t i = 0; i < 16; i++)
state[i] = temp[i];
}
AddRoundKey
라운드 키를 현재 블록에 XOR로 더한다. 매 라운드마다 roundKey의 앞에서부터의 값을 사용한다.
예제 코드에서 roundKey의 자료형은 32bit로 이뤄져 있다. 한 번 AddRoundKey를 수행하는데에 roundKey는 16byte, 128bit가 필요하고, AddRoundKey는 총 11번 (AES-128에서, 초기 1번, 라운드 10번동안 한 번씩 총 11번) 호출되므로 roundKey의 총 사이즈는 44word이다.
void AddRoundKey(uint8_t *state, const uint32_t *roundKey)
{
for (int i = 0; i < 16; i++)
{
state[i] ^= ((uint8_t *)roundKey)[i];
}
}
그래서 roundKey는 어떻게 구하는가? 하면 key를 통해, SubWord와 RotWord라는 연산을 이용하여 만들어진다.
먼저 SubWord는 각 바이트를 sbox값으로 치환한다. 여기서 sbox는 SubBytes에서 사용했던 그 배열이다.
RotWord는 워드의 첫 바이트가 끝으로 이동하고, 나머지는 앞쪽으로 시프트된다.
먼저 key를 첫 번째 roundKey에 복제한다. (key는 8bit단위의 배열, roundKey는 32bit단위의 배열임을 고려한다)
그 이후 아래 과정을 10번 반복한다.
각 roundKey의 맨 처음 word는, 그 직전 word값 W에 대해, SubWord(RotWord(W)) ^ Rcon(now_round)한 값을 이전 라운드의 같은 자리의 word값에 XOR 한 값이다.
그 다음 word부터는 직전 word 값을 이전 라운드와 같은 자리의 word값에 XOR한 값이다.
그렇게 44*uint32_t 크기의 roundKey, 총 11개의 roundKey가 생성된다.
uint8_t Rcon[11] = {0x8d, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36};
...
uint32_t SubWord(uint32_t word)
{
uint32_t result;
result = (sbox[(word)&0xFF]) |
(sbox[(word >> 8) & 0xFF] << 8) |
(sbox[(word >> 16) & 0xFF] << 16) |
(sbox[(word >> 24) & 0xFF] << 24);
return result;
}
uint32_t RotWord(uint32_t word)
{
uint32_t result;
result = (word << 24) | (word >> 8);
return result;
}
void KeyExpansion(const uint8_t *key, uint32_t *roundKey)
{
memset(roundKey, 0, RNDKEYLEN * sizeof(uint32_t));
uint32_t temp;
int i = 0;
while (i < Nk)
{
roundKey[i] = (key[4 * i]) | (key[4 * i + 1] << 8) | (key[4 * i + 2] << 16) | (key[4 * i + 3] << 24);
++i;
}
i = Nk;
while (i < Nb * (Nr + 1))
{
temp = roundKey[i - 1];
if (i % Nk == 0)
{
temp = SubWord(RotWord(temp)) ^ Rcon[i / Nk];
}
roundKey[i] = roundKey[i - Nk] ^ temp;
i += 1;
}
}
AES
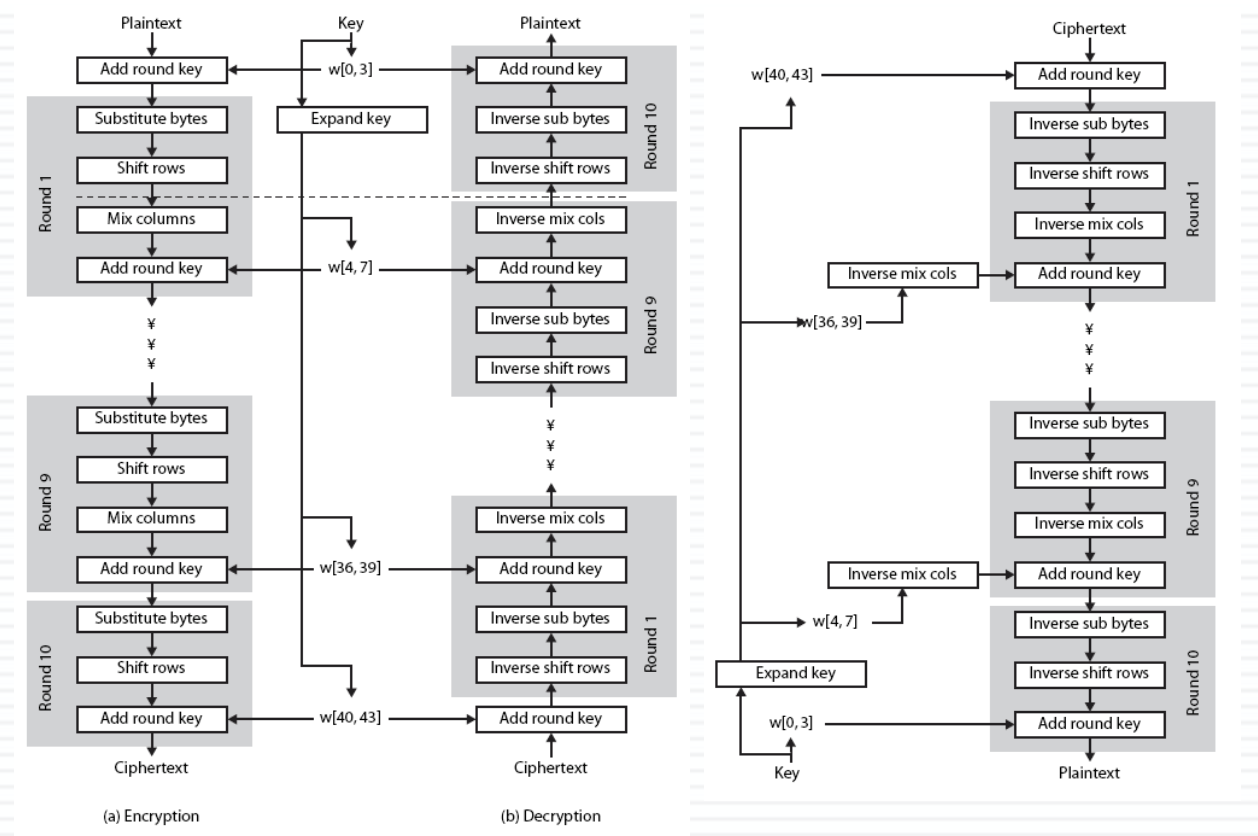
암호화는 라운드 시작 전 AddRoundKey를 먼저 수행하고,
SubBytes -> ShiftRows -> MixColumns -> AddRoundKey를 10라운드까지 반복한다. 단, 마지막 라운드에서는 MixColumns는 수행하지 않는다.
복호화는 라운드 시작 전 AddRoundKey를 먼저 수행하고,
InvSubBytes -> InvShiftRows -> AddRoundKey -> InvMixColumns를 10라운드까지 반복한다. 단, 마지막 라운드에서는 MixColumns는 수행하지 않는다.
순서가 같은 이유는, 원래대로라면 완전한 역순으로 뒤에서부터
AddRoundKey -> InvShiftRows -> InvSubBytes->AddRoundKey->InvMixColumn-> ...를 수행해야 했지만,
여기서 ShiftRows와 SubBytes는 순서를 바꿔도 무관하다. 치환하고 섞나 섞고 치환하나 결과는 같기 때문이다.
그러므로 암호화와 복호화는 거의 같은 회로에서 동작이 가능하다. 따라서 8비트 CPU에서 작동할 정도로 효율적이다.
'학교강의필기장 > 암호학' 카테고리의 다른 글
| 5. Random Number (2) | 2023.10.16 |
|---|---|
| 4. DES, block/stream cipher mode (0) | 2023.10.15 |
| 2. 모듈러 연산 (1) | 2023.10.10 |
| 1. 고전 암호화 기법들 (0) | 2023.09.07 |
| 0. 암호학 개요 (0) | 2023.09.04 |
AES는 DES(Data Encryption Standard)의 취약성을 해결하기 위해 탄생하였다.
Triple DES로 보안을 강화할 수 있었지만, 느리고 블록 크기가 작아서 사용에 제약이 있었다.
그렇게 채택된 암호화 표준인 라인달(Rijndael) 알고리즘이 AES가 되었다.
라인달 암호는 128/192/256 bit key와 128 bit data block을 사용한다.
라인달 암호는 Feistel 구조(데이터 블록을 두 부분으로 나누고 한 부분만 암호화) 대신 반복형 암호를 사용하며 4*4 바이트 블록을 여러 라운드에 걸쳐 처리한다.각 라운드에 전체 데이터 블록에 연산을 적용한다.
AES는 4가지 연산으로 이뤄진다.
1. SubBytes : 각 바이트를 S-box라는 미리 정의된 테이블을 사용해 치환한다.
2. ShiftRows: 블록의 각 행을 다른 양으로 순환 시프트한다.
3. MixColumns: 블록의 각 열을 선형 변환한다.
4. AddRoundKey: 라운드 키를 현재 블록에 XOR연산으로 더한다.
각 연산 방법 세부 사항에 대해 알아보자. 아래 내용은 AES-128을 기반으로 한다.
그 전에, 예제 코드에서 다루는 4*4 바이트 블록의 인덱싱 순서는 다음과 같다.

SubBytes
SubBytes는 현재 상태의 각 바이트를 S-box라는 미리 정의된 테이블을 사용해 치환한다. 복호화를 위해서 Inverse S-box도 필요하다.
구현은 간단하게, 4*4로 이뤄진 현재 상태에 모드에 따라 sbox로 치환하거나 isbox로 치환한다.
sbox와 isbox의 값은 https://en.wikipedia.org/wiki/Rijndael_S-box를 참조하자.
sbox = {...};
isbox = {...};
...
void SubBytes(uint8_t *state, int mode)
{
for (int i = 0; i < 16; i++)
{
state[i] = (mode == ENCRYPT) ? sbox[state[i]] : isbox[state[i]];
}
}
ShiftRows
블록의 각 행을 다른 양으로 순환 시프트한다. 첫 번째 행은 시프트하지 않고, 두 번째 행은 1만큼 왼쪽으로 시프트, 세 번째 행은 2, 네 번째 행은 3만큼 왼쪽으로 시프트한다. 복호화 할 때는 반대 방향으로 시프트 한다.
void ShiftRows(uint8_t *state, int mode)
{
uint8_t temp;
if (mode == ENCRYPT)
{
temp = state[1]; state[1] = state[5]; state[5] = state[9];
state[9] = state[13]; state[13] = temp;
temp = state[2]; state[2] = state[10]; state[10] = temp;
temp = state[6]; state[6] = state[14]; state[14] = temp;
temp = state[3]; state[3] = state[15]; state[15] = state[11];
state[11] = state[7]; state[7] = temp;
}
else
{
temp = state[1]; state[1] = state[13]; state[13] = state[9];
state[9] = state[5]; state[5] = temp;
temp = state[2]; state[2] = state[10]; state[10] = temp;
temp = state[6]; state[6] = state[14]; state[14] = temp;
temp = state[3]; state[3] = state[7]; state[7] = state[11];
state[11] = state[15]; state[15] = temp;
}
}
MixColumns
블록의 각 열을 선형 변환한다. 먼저 암호화를 할 때는 다음 행렬과 GF(2^8)에서 행렬곱을 수행한다.
[2 3 1 1]
[1 2 3 1]
[1 1 2 3]
[3 1 1 2]여기서 2로 곱하는 것은 왼쪽 비트시프트를 1만큼 수행하고, 오버플로우 발생 시 불가역다항식과 XOR연산을 한다.
3으로 곱하는 것은 2로 곱한 결과에 원래 값과 XOR연산을 한다.
AES에서 불가역다항식은 x^8 + x^4 + x^3 + x + 1 이다. 이를 GF(2^8)에서 나타내면 00011011(2) = 1b(16)이다.
따라서 2로 곱하는 것은 (((a) << 1) ^ (((a >> 7) & 1) * 0x1b)) 로 나타낼 수 있다.
복호화를 할 때는 위 행렬의 GF(2^8)에서의 역행렬을 사용한다.
[14 11 13 9]
[ 9 14 11 13]
[13 9 14 11]
[11 13 9 14]다음 행렬을 사용하게 되는데, 9,11,13,14의 곱을 수행해야 한다. 곱해야 하는 값을 a라고 할 때,
9a = 2*2*2*a + a
11a = 2*2*2*a + a + 2*a
13a = 2*2*2*a + a + 2*2*a
14 a = 2*2*2*a + 2*a + 2*2*a
로 나타낼 수 있다. 따라서 암호화에서 사용했던 연산 방법을 그대로 사용하여 연산할 수 있다.
아래 코드에서 사용한 M, IM은 행렬곱을 편리하게 하기 위해 전치행렬로 나타낸 상태이다.
#define XTIME(a) (((a) << 1) ^ (((a >> 7) & 1) * 0x1b))
...
uint8_t M[16] = {2, 3, 1, 1, 1, 2, 3, 1, 1, 1, 2, 3, 3, 1, 1, 2};
uint8_t IM[16] = {0x0e, 0x0b, 0x0d, 0x09, 0x09, 0x0e, 0x0b, 0x0d, 0x0d, 0x09, 0x0e, 0x0b, 0x0b, 0x0d, 0x09, 0x0e};
...
void MixColumns(uint8_t *state, int mode)
{
uint8_t temp[16] = {};
for (uint8_t i = 0; i < BLOCKLEN; ++i)
{
uint8_t x = i / Nb, y = i % Nb;
for (int k = y * 4; k < y * 4 + 4; ++k)
{
uint8_t mul = (mode == ENCRYPT ? M[k] : IM[k]);
if (mul == 1)
{
temp[x * 4 + y] ^= state[x * 4 + k % 4];
}
else if (mul <= 3)
{
temp[x * 4 + y] ^= XTIME(state[x * 4 + k % 4]);
if (mul == 3)
{
temp[x * 4 + y] ^= state[x * 4 + k % 4];
}
}
else
{
temp[x * 4 + y] ^= XTIME(XTIME(XTIME(state[x * 4 + k % 4])));
if (mul == 9 || mul == 11 || mul == 13)
{
temp[x * 4 + y] ^= state[x * 4 + k % 4];
}
if (mul == 11 || mul == 14)
{
temp[x * 4 + y] ^= XTIME(state[x * 4 + k % 4]);
}
if (mul == 13 || mul == 14)
{
temp[x * 4 + y] ^= XTIME(XTIME(state[x * 4 + k % 4]));
}
}
}
}
for (uint8_t i = 0; i < 16; i++)
state[i] = temp[i];
}
AddRoundKey
라운드 키를 현재 블록에 XOR로 더한다. 매 라운드마다 roundKey의 앞에서부터의 값을 사용한다.
예제 코드에서 roundKey의 자료형은 32bit로 이뤄져 있다. 한 번 AddRoundKey를 수행하는데에 roundKey는 16byte, 128bit가 필요하고, AddRoundKey는 총 11번 (AES-128에서, 초기 1번, 라운드 10번동안 한 번씩 총 11번) 호출되므로 roundKey의 총 사이즈는 44word이다.
void AddRoundKey(uint8_t *state, const uint32_t *roundKey)
{
for (int i = 0; i < 16; i++)
{
state[i] ^= ((uint8_t *)roundKey)[i];
}
}
그래서 roundKey는 어떻게 구하는가? 하면 key를 통해, SubWord와 RotWord라는 연산을 이용하여 만들어진다.
먼저 SubWord는 각 바이트를 sbox값으로 치환한다. 여기서 sbox는 SubBytes에서 사용했던 그 배열이다.
RotWord는 워드의 첫 바이트가 끝으로 이동하고, 나머지는 앞쪽으로 시프트된다.
먼저 key를 첫 번째 roundKey에 복제한다. (key는 8bit단위의 배열, roundKey는 32bit단위의 배열임을 고려한다)
그 이후 아래 과정을 10번 반복한다.
각 roundKey의 맨 처음 word는, 그 직전 word값 W에 대해, SubWord(RotWord(W)) ^ Rcon(now_round)한 값을 이전 라운드의 같은 자리의 word값에 XOR 한 값이다.
그 다음 word부터는 직전 word 값을 이전 라운드와 같은 자리의 word값에 XOR한 값이다.
그렇게 44*uint32_t 크기의 roundKey, 총 11개의 roundKey가 생성된다.
uint8_t Rcon[11] = {0x8d, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36};
...
uint32_t SubWord(uint32_t word)
{
uint32_t result;
result = (sbox[(word)&0xFF]) |
(sbox[(word >> 8) & 0xFF] << 8) |
(sbox[(word >> 16) & 0xFF] << 16) |
(sbox[(word >> 24) & 0xFF] << 24);
return result;
}
uint32_t RotWord(uint32_t word)
{
uint32_t result;
result = (word << 24) | (word >> 8);
return result;
}
void KeyExpansion(const uint8_t *key, uint32_t *roundKey)
{
memset(roundKey, 0, RNDKEYLEN * sizeof(uint32_t));
uint32_t temp;
int i = 0;
while (i < Nk)
{
roundKey[i] = (key[4 * i]) | (key[4 * i + 1] << 8) | (key[4 * i + 2] << 16) | (key[4 * i + 3] << 24);
++i;
}
i = Nk;
while (i < Nb * (Nr + 1))
{
temp = roundKey[i - 1];
if (i % Nk == 0)
{
temp = SubWord(RotWord(temp)) ^ Rcon[i / Nk];
}
roundKey[i] = roundKey[i - Nk] ^ temp;
i += 1;
}
}
AES

암호화는 라운드 시작 전 AddRoundKey를 먼저 수행하고,
SubBytes -> ShiftRows -> MixColumns -> AddRoundKey를 10라운드까지 반복한다. 단, 마지막 라운드에서는 MixColumns는 수행하지 않는다.
복호화는 라운드 시작 전 AddRoundKey를 먼저 수행하고,
InvSubBytes -> InvShiftRows -> AddRoundKey -> InvMixColumns를 10라운드까지 반복한다. 단, 마지막 라운드에서는 MixColumns는 수행하지 않는다.
순서가 같은 이유는, 원래대로라면 완전한 역순으로 뒤에서부터
AddRoundKey -> InvShiftRows -> InvSubBytes->AddRoundKey->InvMixColumn-> ...를 수행해야 했지만,
여기서 ShiftRows와 SubBytes는 순서를 바꿔도 무관하다. 치환하고 섞나 섞고 치환하나 결과는 같기 때문이다.
그러므로 암호화와 복호화는 거의 같은 회로에서 동작이 가능하다. 따라서 8비트 CPU에서 작동할 정도로 효율적이다.
'학교강의필기장 > 암호학' 카테고리의 다른 글
| 5. Random Number (2) | 2023.10.16 |
|---|---|
| 4. DES, block/stream cipher mode (0) | 2023.10.15 |
| 2. 모듈러 연산 (1) | 2023.10.10 |
| 1. 고전 암호화 기법들 (0) | 2023.09.07 |
| 0. 암호학 개요 (0) | 2023.09.04 |
