symmetric key, 대칭키는 키를 하나만 사용하는 암호화에서 사용한다.
암호문을 보내는 사람과 푸는 사람 모두 같은 키를 가지고 있어야 하며, 전자서명이 안되기 때문에 메시지를 위조하거나 내가 안보냈는데 보냈다고 하는 등 문제가 발생할 수 있다. (유용하지 않다는 뜻이 아니다.)
Public-Key Cryptography
Asymmetric key => public key + private key
공개키 시스템은 공개키와 개인키가 있고, 공개키는 모두에게 보여져도 상관없고 개인키는 숨긴다.
공개키로 암호화했다면 개인키로 풀 수 있고, 개인키로 암호화했다면 공개키로 풀 수 있다.
장점으로는 다음과 같다.
1. 키 분배 문제를 해결할 수 있다. 상대방에게 공개키만 보내주면 되고, 대칭키 시스템의 키 또한 이 방법으로 전송하면 안전하다.
2. 전자서명이 가능하다. 개인키는 나만 가지고 있으므로, 개인키로 암호화 했다는 뜻은 내가 암호화 했다고 증명하는 것이다.
3. 보안이 제공되는 암복호화가 가능하다.
단점으로는 느리다.

위 예시에서, Bob은 Alice의 공개키, PUa를 가지고 있고, Alice는 자신의 개인키, PRa를 가지고 있다.
Bob은 보내려는 메세지 X를 PUa로 암호화하여 암호문 Y를 전송한다. => Y = E[PUa, X]
Alice는 받은 메세지 Y를 PRa로 복호화하여 읽을 수 있다. => X = D[PRa, Y]
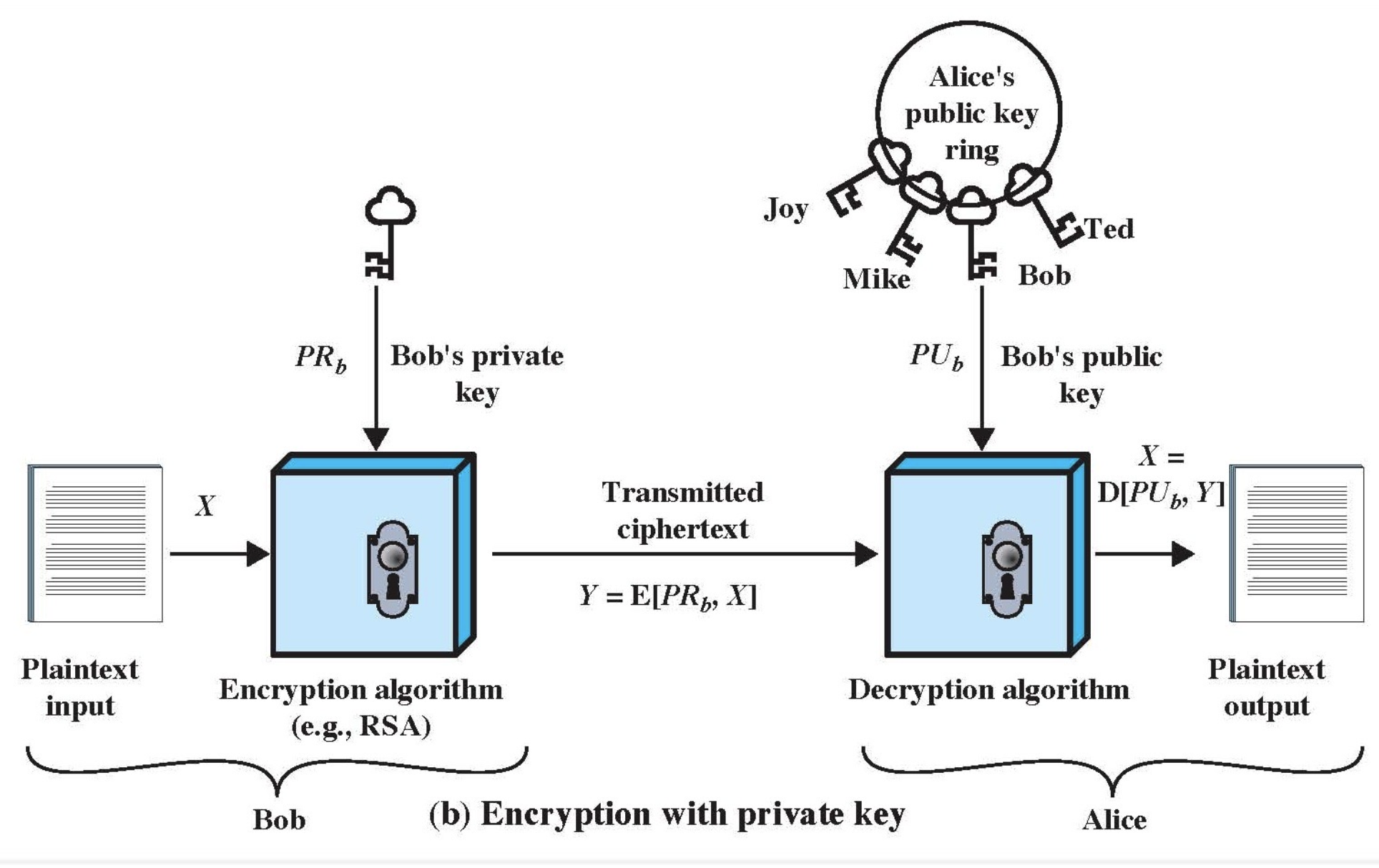
위에서는 Bob은 자신의 개인키, PRb를 가지고 있고 Alice는 Bob의 공개키 PUb를 가지고 있다.
Bob은 보내려는 메세지 X를 PRb로 암호화하여 암호문 Y를 전송한다. => Y = E[PRb, X]
Alice는 받은 메세지 Y를 PUb로 복호화하여 읽을 수 있다. => X = D[PUb, Y]
이 때, 개인키로 전송한 메세지가 탈취당해 동일한 공개키를 가진 사람이 읽을 수도 있다.
이를 해결하는 방법은 다음과 같다.

1. A는 메세지 X를 PRa로 암호화하여 암호문 Y를 만든다. => 전자서명
2. A는 암호문 Y를 PUb로 다시 암호화하여 암호문 Z를 만든다. => 암호화
3. A는 B에게 암호문 Z를 전송한다.
4. B는 암호문 Z를 PRb로 복호화하여 암호문 Y를 만든다. => 복호화
5. B는 암호문 Y를 PUa로 복호화하여 평문 X를 읽을 수 있다. => 신원확인
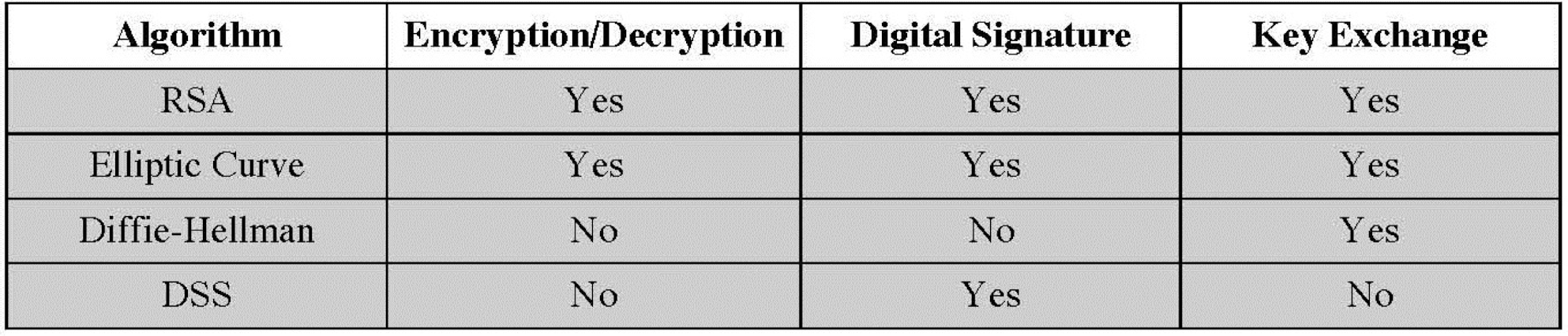
위 모든 기능을 하는 알고리즘도 있지만, 몇몇의 알고리즘은 특정 기능만 수행한다.
Diffie-Hellman 알고리즘은 키분배(주로 대칭키를 보냄)만을 위한 알고리즘이다.
DSS는 전자서명만을 위한 알고리즘이다.
RSA
알고리즘과 암호키가 있어도 복호키를 아는 것은 계산적으로 어려워야하며, 두 키가 있다면 계산이 쉬워야 한다.
두 키 중 하나를 공개키로, 하나를 개인키로 사용한다.
=> trapdoor one-way function이 필요하다.
X를 Y로 변환하긴 쉽지만, Y를 X로 계산하기 어려운 것을 one-way function이라 한다. (hash 등)
반면 trapdoor one-way function은 key가 있다면 X와 Y의 상호간 변환이 쉽다.
반면 key가 없다면 변환이 어려워야 한다.
이를 위해 우리는 큰 소수의 곱을 사용한다.
n=pq라고 할 때, p와 q를 둘 다 모르면 어떤 수인지 알아내기 현실적으로 어렵다.
따라서 RSA 암복호화를 위한 절차는 다음과 같다.
1. 큰 랜덤 소수 p와 q를 얻는다.
2. n = pq이다.
3. ø(n) = ø(pq) = (p-1)(q-1) 이다.
4. 1 < e < ø(n)인 랜덤한 소수 암호화키 e를 고른다. (반드시 소수일 필요는 없다. 단, gcd(e, ø(n))=1을 만족해야 한다.)
5. ed = 1 mod ø(n) 를 만족하는 d를 구한다. 즉, d = e^-1이다.
여기서 n과 더불어 e는 공개키, d는 개인키가 된다.
평문 M, 암호문 C에 대하여
PU = {e, n}; C = M^e mod n
PR = {d, n}; M = C^d mod n
이 된다.
소수 e와 d로써 암복호화를 할 수 있음이 어떻게 증명될까?
오일러 법칙에 따라, r ≡ s (mod ø(n)), 모든 a에 대해 a^r ≡ a^s (mod n) 이다.
e는 1~ø(n) 사이에서 구했고, d는 e의 mod ø(n)에 대한 역이다.
즉, ed ≡ 1 (mod ø(n))이다.
따라서 모든 k에 대하여 ed = 1+kø(n)이다.
C = M^e mod n; M = C^d mod n
이였다. M = C^d mod n 부터 증명해보자.
C^d mod n
= M^ed mod n
= M^(1+kø(n)) mod n
k=0, M mod n = M
C = M^e mod n도 같은 방법으로 증명할 수 있기에 생략하겠다.
최적화 방법
암복호화 과정에서 필요한 제곱은 이전에도 다룬 Sqaure and Multiply Algorithm을 사용하여 빠르게 수행할 수 있다.
y = x^n이라고 할 때, n을 비트단위로 두고, 최하단 비트로부터 순회하며 제곱수를 곱해준다.
y = 1;
while(n>0){
if(n&1) y = y*x;
x = x*x;
n = n>>1;
}
e가 작을수록 지수화 연산이 더 빠르게 수행된다. 따라서 작은 e값을 선택하면 암호화 과정이 더욱 효율적이게 된다.
흔히 사용되는 e 값은 65537(2^16+1)이다.
다만, e가 너무 작으면 CTR과 같은 방법으로 공격을 받을 수 있으므로 적절한 값을 선택해야 한다.
반면 d는 큰 값을 사용해야 한다. 그렇지 않으면 보안이 취약해질 수 있다.
중국인의 나머지 정리(CTR)을 사용하여 복호화를 개선할 수 있다. p와 q에 대해 따로 계산을 수행하고 결과를 합친다. 일반적으로 4배정도 더 빠르다.
n = pq라 할 때, M = C^d mod n 를 계산해보자.
CRT를 하기 전, 더욱 최적화하기 위해 d제곱을 축소화한다.
dP = d mod (p-1), dQ = d mod (q-1) 이다.
C^d mod p = C^dP mod p를 증명하면,
d = dP + k(p-1) 이다.
C^d = C^(dP + k(p-1)) = (C^(p-1))^k * C^dP
여기서 p-1은 ø(p)이기 때문에, 오일러의 소정리에 따라 (C^(p-1))^k ≡ 1^k (mod p)
양변에 C^dP를 곱해주면 (C^(p-1))^k * C^dP ≡ 1^k * C^dP (mod p)
따라서 C^d mod p = C^dP mod p 이다.
아래로는 CRT를 연산한다. n = pq이기에 p와 q로 분리한다.
m_1 = C^dP mod p; m_2 = C^dQ mod q
M_1 = n/p = q
M_2 = n/q = p
M = m_1 * q(q^-1 mod p) + m_2 * p(p^-1 mod q)
여기서, 확장 유클리드 알고리즘에 따라 서로소 p,q에 대해
1 = p * (p^-1 mod q) + q * (q^-1 mod p)
p(p^-1 mod q) = 1 - q(q^-1 mod p)
이를 M에 대한 식에 대입하면,
M = m_1 * q(q^-1 mod p) + m_2(1 - q(q^-1 mod p))
= m_1 * q(q^-1 mod p) + m_2 - m_2 * q(q^-1 mod p)
= m_2 + q(m_1 + m_2)(q^-1 mod p)
가 된다.
따라서 RSA의 개인키는 실제로는 (p, q, dP, dQ, qInv) 를 저장해둔다.
복호화 과정에서는
m_1 = C^dP mod p
m_2 = C^dQ mod q
M = m_2 + q(m_1 - m_2) * (q^-1 mod p)
만 수행하게 된다.
보안
브루트포스 공격으로는 현실적으로 RSA를 파훼하기 어렵다.
인수분해를 이용한 방법, 타이밍 공격, 선택된 암호문 공격(chosen ciphertext attack)이 있다.
n을 p와 q로 인수분해하면 ø(n)을 쉽게 계산할 수 있다. ø(n)를 알면 d도 계산할 수 있게 된다.
ø(n)를 직접 결정하여 d를 계산하거나 공개키를 이용해 d를 찾는 방법은 불가능에 가깝다.
현재는 2048bit의 RSA가 인수분해 공격으로부터 안전하다고 알려져 있다.
또, p와 q가 비슷한 크기일 수록 안전하고 Carmichael's totient function, 𝜆(n)을 사용하는 것이 안전하다.
𝜆(n) = lcm(p-1, q-1)이다.
타이밍 공격은 암호화 연산의 실행 시간의 변동을 분석해서 정보를 추출하는 방법이다.
이를 막기 위해, 모든 연산에 대해 일정한 시간이 걸리도록 거듭제곱 연산을 수행하거나, 랜덤 지연을 추가하거나, 계산에 사용되는 값을 숨기는(변형하는) 방법이 있다.
CCA(chosen ciphertext attack)는 특정한 암호문을 선택하고 그것을 복호화하게 해서 암호를 분석한다.
RSA는 이에 취약한데, Epu(M1) * Epu(M2) = Epu(M1 * M2)로, M1과 M2의 공개키로의 암호화를 곱하면 M1과 M2의 곱의 암호화와 같아진다.
공격자는 주어진 암호문 C를 받아 C를 수정하여 새로운 암호문 X를 생성한다.
이 X는 복호화되면 2M mod n을 결과로 제공한다. 그래서 공격자는 M을 추론할 수 있다.
이를 해결하기 위해 평문에 무작위 패딩을 추가하거나 최적 비대칭 암호화 패딩 (OAEP) 를 사용할 수 있다.
OAEP
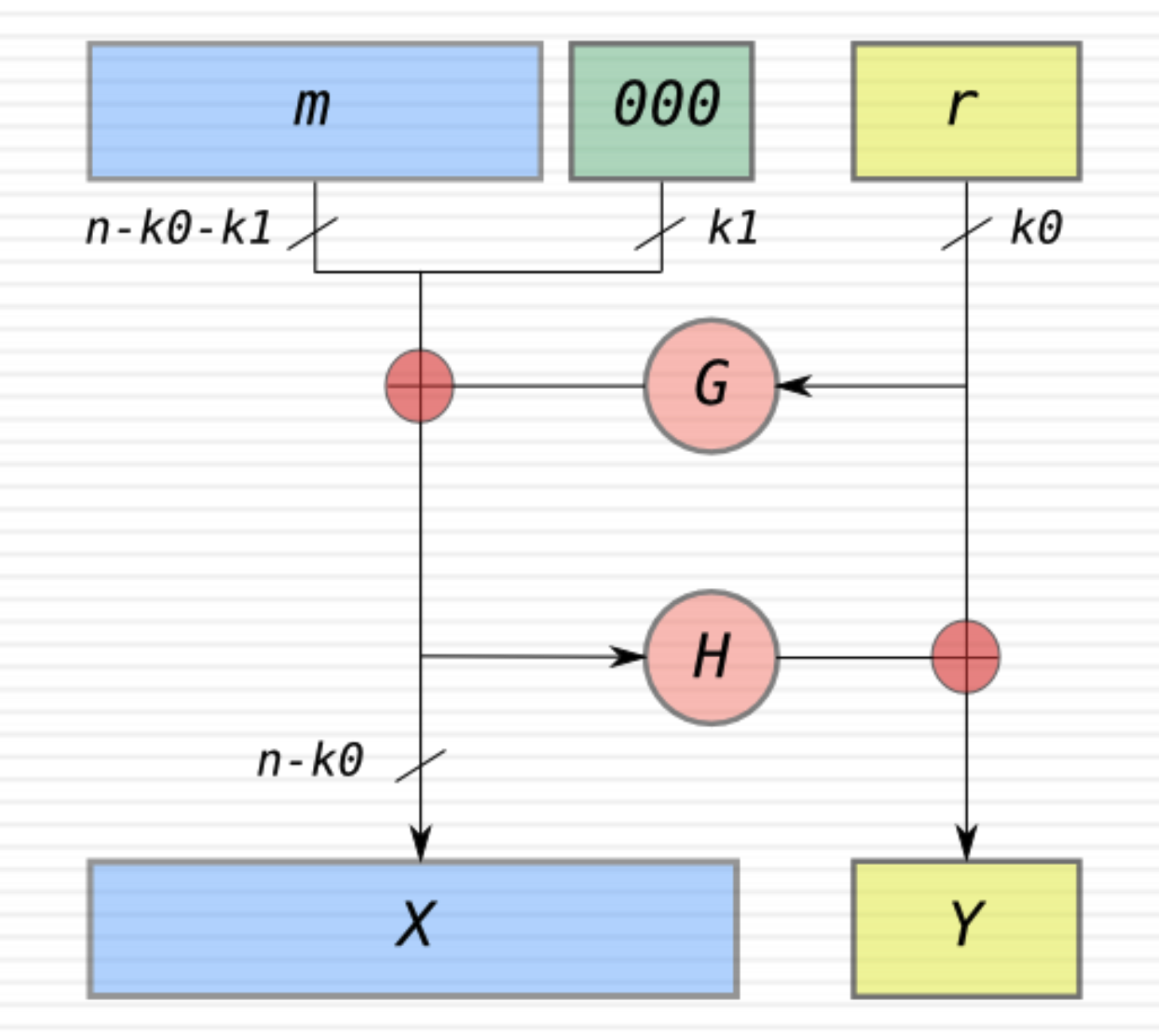
m은 original message, 000은 패딩, r은 랜덤한 스트링이다.
G와 H는 one-way function 또는 hash function이다. (즉, 단방향이다)
m + padding에 G(r)을 XOR한 값을 X에, H(X)와 r을 XOR한 값을 Y에 넣는다.

RSA에서의 OAEP는 위와 같다.
상단 좌측으로부터, 00은 모듈러 연산으로부터 오버플로우를 방지하기 위함이다.
seed는 랜덤 넘버이고, lHash는 label hash, PS는 padding string, 그리고 01은 구분자이다. 그 뒤로 Message가 들어간다.
결과값으로는 오버플로우 방지용 00은 그대로 내려간다.
S = lHash + PS +01 + M 라 할 때, maskedDB = MGF(seed) XOR S 이다. 여기서 MGF는 mask generation functions이다.
maskSeed = maskedDB XOR seed 이다.
이러한 모델을 사용함으로써 CCA를 막을 수 있다.
'학교강의필기장 > 암호학' 카테고리의 다른 글
| 9. 키 교환 알고리즘과 암복호화 알고리즘, 그리고 타원곡선 (1) | 2023.12.06 |
|---|---|
| 8. 모듈러/정수론 정리 (1) | 2023.10.20 |
| 6. number theory (1) | 2023.10.17 |
| 5. Random Number (2) | 2023.10.16 |
| 4. DES, block/stream cipher mode (0) | 2023.10.15 |
