GCD (Greatest Common Divisor)
최대 공약수란 두 개 이상의 정수 간의 가장 큰 공통된 약수를 뜻한다.
relatively prime(서로소)란 최대 공약수가 1인 정수쌍이다.
만약 GCD(a,0)이라면 최대 공약수는 a이다. GCD(0,0)은 정의되지 않는다.
gcd(a,b) = gcd(b, a%b) 라는 원리를 이용한 유클리드 알고리즘을 통해 GCD를 구할 수 있다.
Euclid(a,b){
while (a != 0 && b != 0)
{
int n = a % b;
a = b;
b = n;
}
return a ? a : b;
}최대 공약수를 구하려는 a,b에 대해, a%b를 구한 값을 b로, a값을 b로 대입하는 과정을 두 정수 중 하나가 0이 될 때까지 반복한다. 만약 둘 중 하나가 0이 된다면 둘 중 0이 아닌 수가 최대 공약수이다.
Modular Arthmetic
나머지 연산에서 나머지를 음수로 나타낼 수도 있지만, 보통 양수로 나타낸다.
a (mod b) 라고 할 때 임의의 정수 n에 대해, a (mod b) = (a + b*n) (mod b)이다.
따라서 -12 (mod 7)은 -5가 될 수도 있지만, 2 (mod 7)과 같은 뜻이므로 2가 될 수 있다.
a와 b가 합동이란 것은 a (mod n) = b (mod n)을 만족함을 뜻한다. 이를 a≡b(mod n)이라 한다.
모듈러의 성질로, (a*b) mod n = ((a mod n) * (b mod n)) mod n이고,
거듭 제곱의 성질로 a^(b+c) = a^b * a^c 와 a^(b*c) = (a^b)^c 가 있다.
만약 17^14 mod 8 을 구한다고 하자. 이는 모듈러의 성질에 따라 ((17 mod 8)^14) mod 8 과 같다.
따라서 ((17 mod 8)^14) mod 8 = 1^14 mod 8 = 1이다.
Group (군)
군 G은 {G,⋅}으로, 이진 연산 ⋅이 정의된 원소의 집합이다. 예를 들어 ⋅가 덧셈이라면, 그 군은 덧셈 군이다.
이는 다음과 같은 공리를 만족해야 한다.
1. Closure(닫힘) : 군 내의 모든 원소 a,b에 대하여 a⋅b 역시 G의 원소여야 한다.
2. Associative(결합법칙) : 군 내의 모든 원소 a,b,c에 대하여 (a⋅b)⋅c = a⋅(b⋅c)를 만족해야 한다.
3. Identity Element(항등원) : 군 G에는 항등원 e가 존재하여, 군 내의 모든 원소 a에 대해 e⋅a = a⋅e = a를 만족해야 한다.
4. Inverse Element (역원) : 군 내의 모든 원소 a에 대하여, 그 역원 a'이 존재해 a⋅a'=e를 만족해야 한다.
만약 군이 교환법칙, 즉 원소 a,b에 대해 a⋅b = b⋅a를 만족한다면 그 군을 아벨 군(Abelian Group)이라고 한다.
만약 n개의 구별 가능한 기호의 집합 Σ에 대한 순열 집합이 있다고 하자. Sn은 Σ의 모든 순열의 집합이다.
1. a*b 역시 Sn의 원소이다.
2. (a*b)*c = a*(b*c) 이다.
3. 항등원이 존재한다.
4. 모든 순열에 대하여 역원이 존재한다.
하지만, a*b != b*a 이므로 아벨군은 아니다.
Find a^-1 mod m
만약 a와 m이 서로소라면 a^-1은 항상 존재한다.
확장 유클리드 알고리즘을 사용하면 a^-1을 구할 수 있는데, 확장 유클리드 알고리즘은 a와 b, 그의 최대공약수 gcd에 대해 gcd = ax+by를 만족하는 x와 y를 구한다. 이 때 x가 a^-1가 된다.
확장 유클리드 알고리즘은 다음과 같다.
int extended_gcd(int a, int b, int *x, int *y)
{
if (b == 0)
{
*x = 1;
*y = 0;
return a;
}
int x1 = *x;
int y1 = *y;
int gcd = extended_gcd(b, a % b, &x1, &y1);
*x = y1;
*y = x1 - (a / b) * y1;
return gcd;
}이름대로 기존의 유클리드 알고리즘을 응용하여 구현한다. gcd를 구하고, 구하는 과정을 역추적하며 x와 y를 계산한다.
b가 0이라면 gcd를 구한 것(a의 값)이고, 이 때의 x와 y는 각각 1, 0이다.
b * x1 + (a%b) * y1 = gcd(b, a%b)에서, a%b = a-b(a//b)이다. 따라서,
b* x1 + (a-b(a//b)) * y1
= b* x1 + a*y1 - b(a//b) * y1
= a*y1 -b(x1 - (a//b) * y1) = gcd(b, a%b)
이를 ax + by = gcd(a,b)꼴로 나타내려면,
x = y1
y = x1 - (a//b) * y1
이 된다.
이와 유사한 방식으로 모듈러 역원을 구하는 mul_inv 알고리즘 또한 구현할 수 있다.
만약 gcd가 1이라면 x가 a의 모듈러 역원 a^-1가 된다.
gcd가 1이 아니라면 역원은 존재하지 않는다.
갈루아 필드 GF(p)
galois field GF(p)는 소수 p에 대해 정의된 유한 필드이다. GF(p)는 0부터 p-1로 이루어진 집합이다. 이 집합의 산술 연산은 모듈러 p 연산을 따른다.
GF(11)은 {0,1,2,...,10}으로 이뤄져있고, 이 집합의 덧셈, 뺄셈, 곱셈 연산은 모두 mod 11로 수행된다.
이는 소수 p에 대해 정의된 유한 필드이므로 항상 곱셈에 대한 역원이 존재한다.
따라서 GF(p) 내의 산술연산은 잘 정돈되어 있으며(well-behaved) 덧셈 뺄셈 곱셈 나눗셈을 범위를 벗어나지 않고 수행할 수 있다.
예를 들어 선형 연립 방정식인
2x - y = 5 <= (1)
3x + 2y = 6 <= (2)
가 있다고 하자.
(1) * 2 + (2) 를 하면 y를 소거해 x를 구할 수 있을 것이다.
7x = 16 mod 11 = 5
x = 5 * 7^(-1) = 5 * 8 = 7
y는 x를 대입하여 구할 수 있다. => y = 9
만약 mod 2라면, 덧셈과 뺄셈은 XOR연산을 통해 수행된다.
0+0 = 0, 1+0 = 1, 0+1 = 1, 1+1 = 0이기 때문이다. 이를 통해 다항식 연산을 할 수 있다.
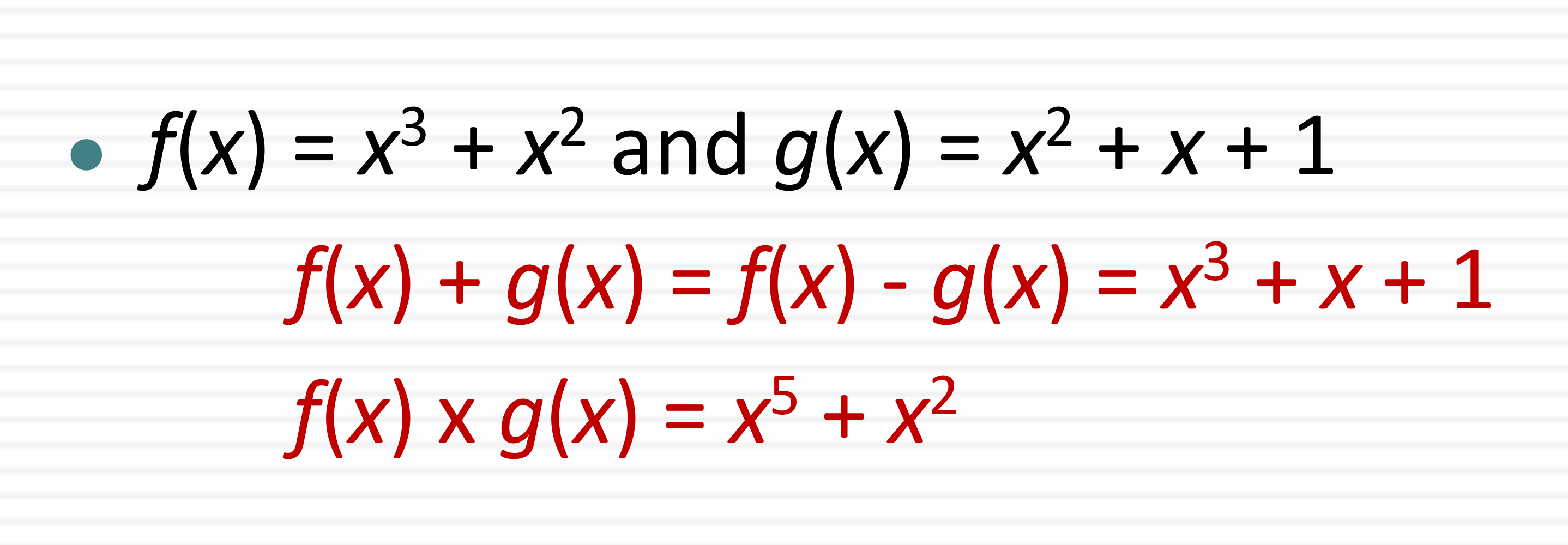
위와같은 연립방정식이 있을 때, 둘을 더함으로 x^3+x+1을 구해낼 수 있다. XOR연산이기 때문에 같은 차수를 더하면 소거되기 때문이다.
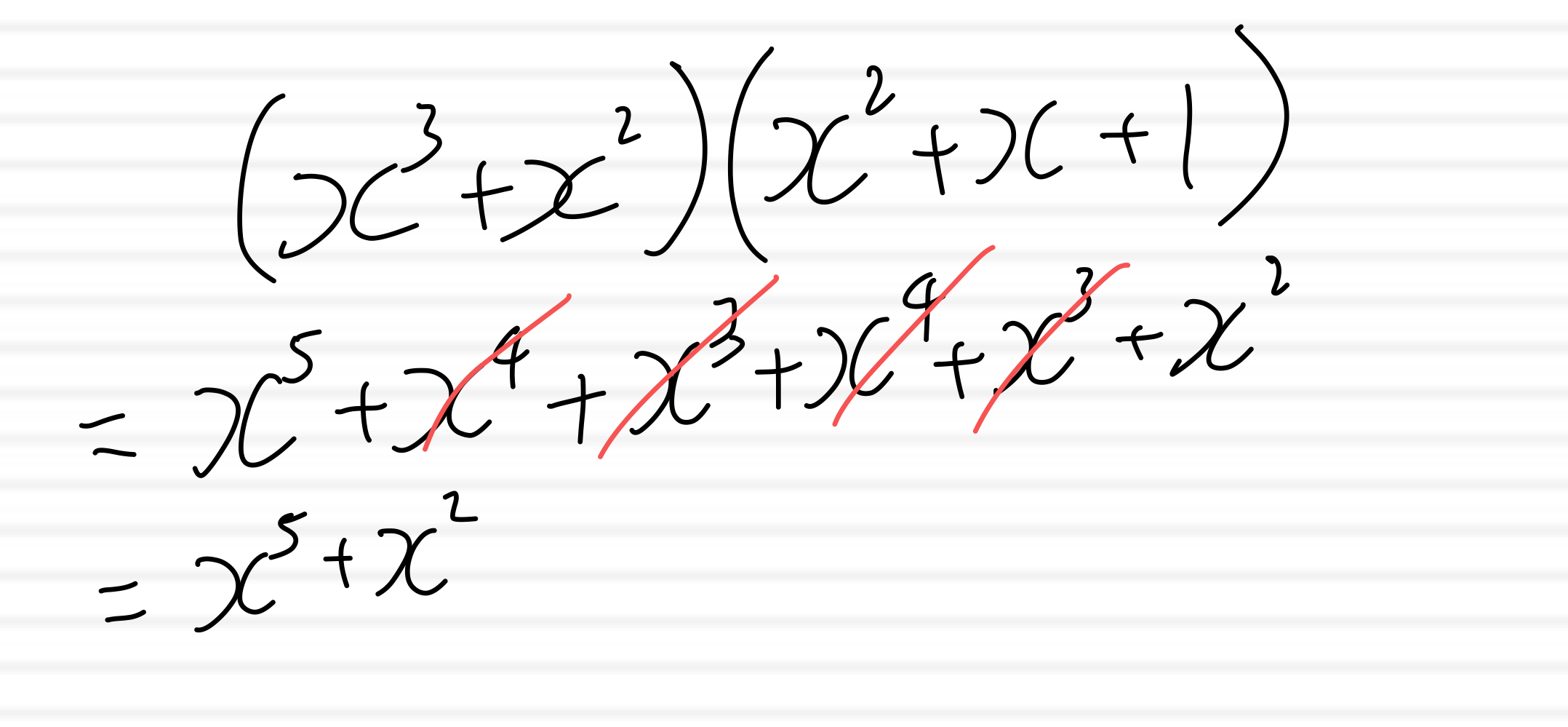
둘을 곱하면 x^5+x^2가 된다.
f(x) = q(x)g(x) + r(x)에서 r(x) = f(x) mod g(x)라고 할 때,
g(x)가 1이나 자기자신으로만 나누어 떨어진다면 g(x)를 irreducible(prime) polynomial(기약 다항식)이라 부른다.
GF(2^n)은, 차수가 n보다 작은 다항식으로 이뤄지며, 연산 이후 기약 다항식으로 나머지 연산을 취한다.
기약 다항식으로 나머지 연산을 취하므로 항상 역이 존재한다.
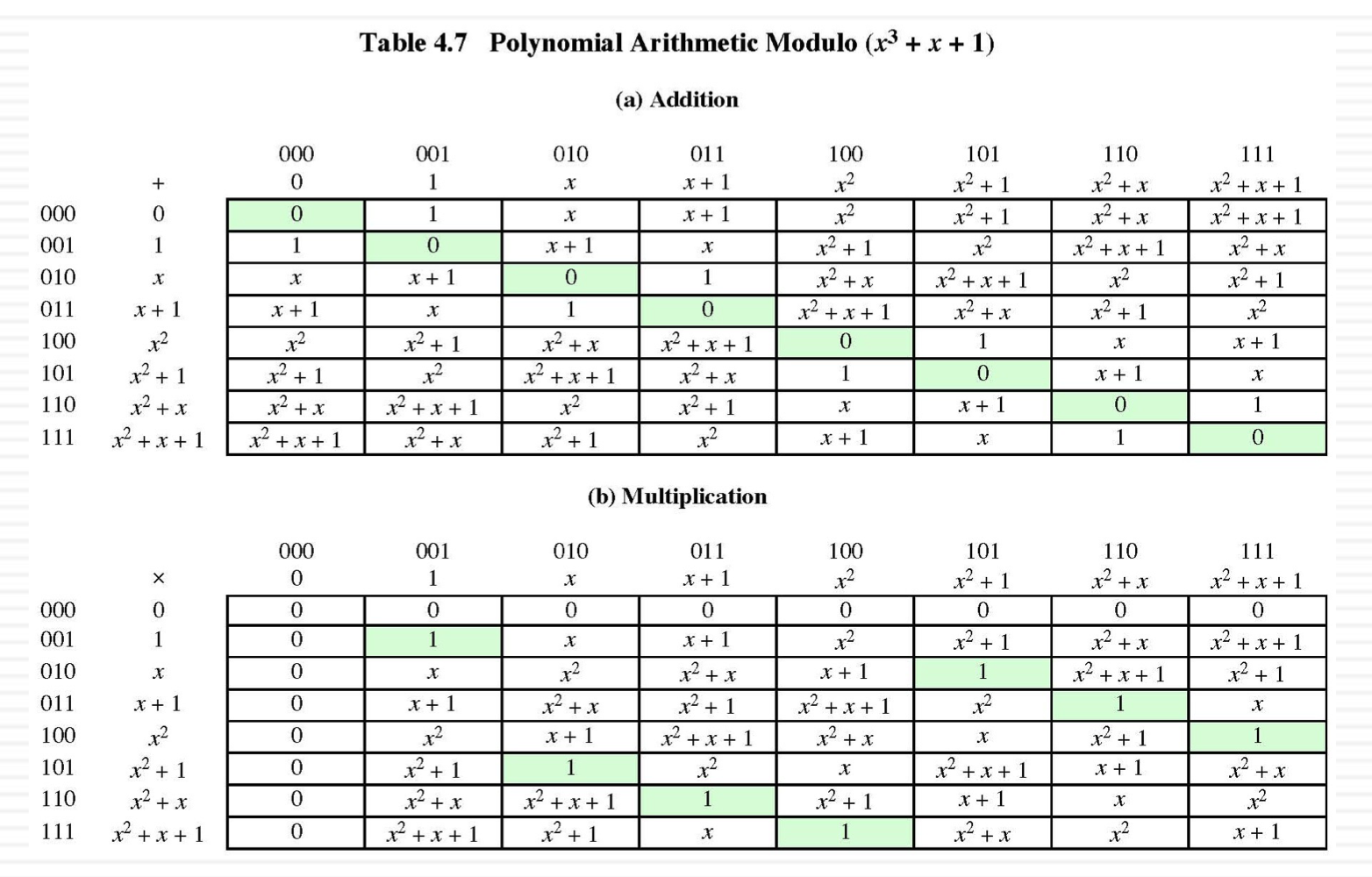
위 테이블은 GF(2^3)에서, 더하기 연산과 곱셈 연산의 결과를 정리한 것이다.
각 다항식은 바이너리로 나타낼 수 있다. 예를 들어 x^2+1은 101이다.
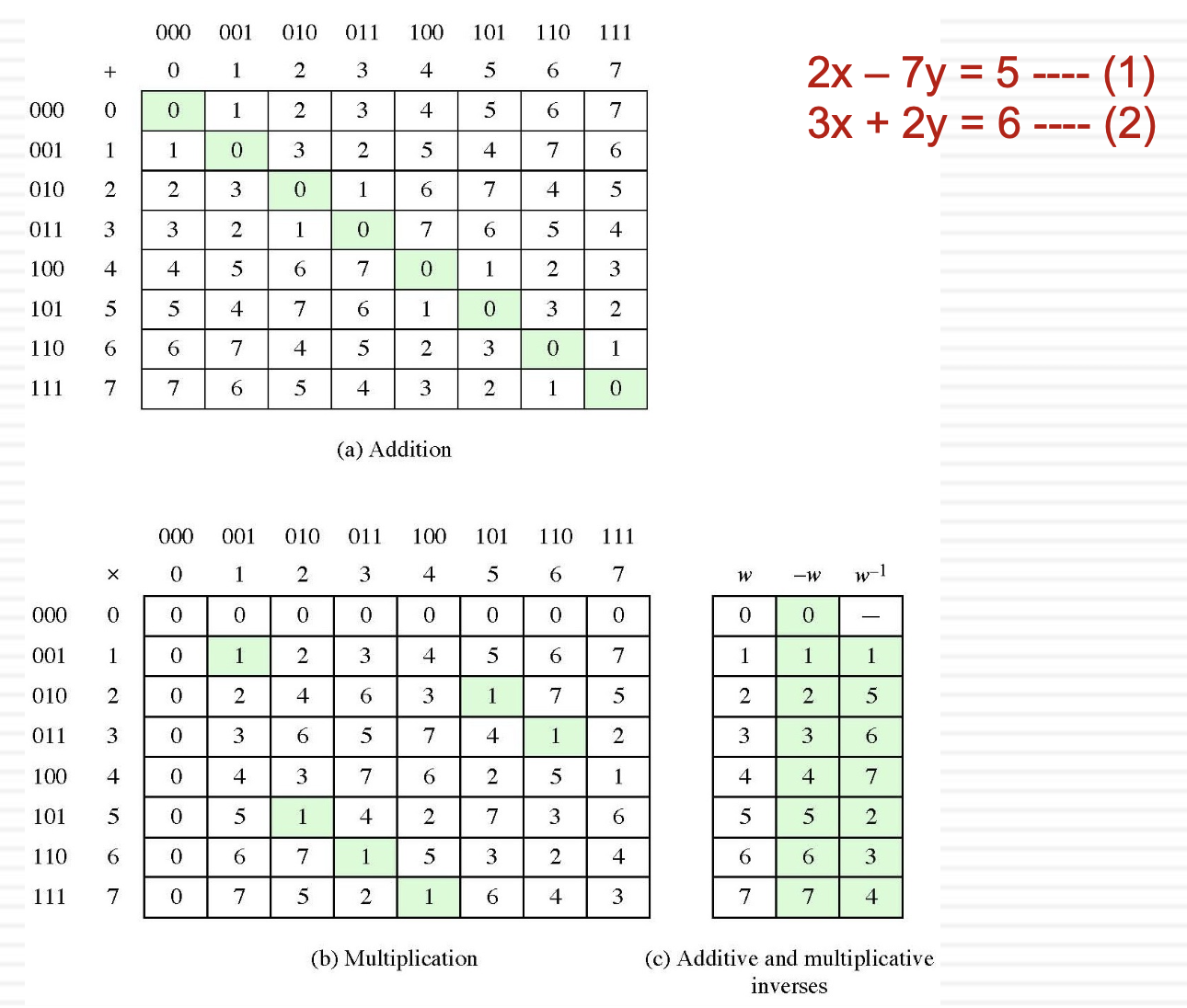
각 다항식을 10진수로 나타내면 위와 같다.
덧셈에서의 역은 자신이다. 곱셈에서의 역은 위 테이블에서 1이 되는 수로, (c)에 정리돼있다.
2x - 7y = 5 <= (1)
3x + 2y = 6 <= (2)
라는 연립방정식을 풀어보자.
(1) + (2)*6이라고 하자, 여기서 곱셈은 위 테이블을 참고한다.
2x - 7y = 5
+ 1x + 7y = 2
=> 3x = 7
x = 7 * 3^(-1) = 7 * 6 = 4
y는 위 식에 대입하여 구할 수 있다. => y = 5
덧셈, 곱셈, 나머지 연산은 XOR연산과 쉬프트 연산으로 할 수 있다.
더하기는 단순히 XOR연산을 통해 구현된다.
곱셈은 먼저 x 곱셈부터 구현하자.
uint8_t xtime(uint8_t x) {
return ((x<<1) ^ ((x>>7) & 1 ? 0x1B : 0));
}위 코드는 GF(2^8) mod x^8+x^4+x^3+x+1 에서의 x 곱셈 함수이다.
x를 곱한다는 것은 각 자리에서 1만큼 왼쪽 쉬프트를 하는 것을 뜻한다.
만약 x가 8bit를 넘어간다면 나머지 연산을 위해 x^4+x^3+x+1을 더해준다.
uint8_t Multiply(uint8_t a, uinit8_t b) {
uint8_t r = 0;
while (b > 0) {
if (b & 1) r = r ^ a;
b = b >> 1;
a = xtime(a);
}
return r;
}위 함수는 xtime 함수를 사용하여 곱셈을 구현한다. 구현 방식은 일반적인 곱셈 방법처럼,
r에는 곱셈의 결과값을 저장한다. b를 가장 낮은 차수인 가장 오른쪽 비트에서부터 왼쪽으로 순회한다. 이는 b=b>>1로 구현되어있다.
만약 현재 순회중인 차수가 존재한다면 (b&1 == 1)이라면, r에 현재 a를 더해준다. 이때 a는 각 차수에 알맞게 곱해져있는 상태이다. 이는 a = xtime(a)로 구현되어있다.
b의 순회가 끝나면 곱셈의 결과가 나온다.
'학교강의필기장 > 암호학' 카테고리의 다른 글
| 5. Random Number (2) | 2023.10.16 |
|---|---|
| 4. DES, block/stream cipher mode (0) | 2023.10.15 |
| 3. AES (0) | 2023.10.12 |
| 1. 고전 암호화 기법들 (0) | 2023.09.07 |
| 0. 암호학 개요 (0) | 2023.09.04 |
GCD (Greatest Common Divisor)
최대 공약수란 두 개 이상의 정수 간의 가장 큰 공통된 약수를 뜻한다.
relatively prime(서로소)란 최대 공약수가 1인 정수쌍이다.
만약 GCD(a,0)이라면 최대 공약수는 a이다. GCD(0,0)은 정의되지 않는다.
gcd(a,b) = gcd(b, a%b) 라는 원리를 이용한 유클리드 알고리즘을 통해 GCD를 구할 수 있다.
Euclid(a,b){
while (a != 0 && b != 0)
{
int n = a % b;
a = b;
b = n;
}
return a ? a : b;
}최대 공약수를 구하려는 a,b에 대해, a%b를 구한 값을 b로, a값을 b로 대입하는 과정을 두 정수 중 하나가 0이 될 때까지 반복한다. 만약 둘 중 하나가 0이 된다면 둘 중 0이 아닌 수가 최대 공약수이다.
Modular Arthmetic
나머지 연산에서 나머지를 음수로 나타낼 수도 있지만, 보통 양수로 나타낸다.
a (mod b) 라고 할 때 임의의 정수 n에 대해, a (mod b) = (a + b*n) (mod b)이다.
따라서 -12 (mod 7)은 -5가 될 수도 있지만, 2 (mod 7)과 같은 뜻이므로 2가 될 수 있다.
a와 b가 합동이란 것은 a (mod n) = b (mod n)을 만족함을 뜻한다. 이를 a≡b(mod n)이라 한다.
모듈러의 성질로, (a*b) mod n = ((a mod n) * (b mod n)) mod n이고,
거듭 제곱의 성질로 a^(b+c) = a^b * a^c 와 a^(b*c) = (a^b)^c 가 있다.
만약 17^14 mod 8 을 구한다고 하자. 이는 모듈러의 성질에 따라 ((17 mod 8)^14) mod 8 과 같다.
따라서 ((17 mod 8)^14) mod 8 = 1^14 mod 8 = 1이다.
Group (군)
군 G은 {G,⋅}으로, 이진 연산 ⋅이 정의된 원소의 집합이다. 예를 들어 ⋅가 덧셈이라면, 그 군은 덧셈 군이다.
이는 다음과 같은 공리를 만족해야 한다.
1. Closure(닫힘) : 군 내의 모든 원소 a,b에 대하여 a⋅b 역시 G의 원소여야 한다.
2. Associative(결합법칙) : 군 내의 모든 원소 a,b,c에 대하여 (a⋅b)⋅c = a⋅(b⋅c)를 만족해야 한다.
3. Identity Element(항등원) : 군 G에는 항등원 e가 존재하여, 군 내의 모든 원소 a에 대해 e⋅a = a⋅e = a를 만족해야 한다.
4. Inverse Element (역원) : 군 내의 모든 원소 a에 대하여, 그 역원 a'이 존재해 a⋅a'=e를 만족해야 한다.
만약 군이 교환법칙, 즉 원소 a,b에 대해 a⋅b = b⋅a를 만족한다면 그 군을 아벨 군(Abelian Group)이라고 한다.
만약 n개의 구별 가능한 기호의 집합 Σ에 대한 순열 집합이 있다고 하자. Sn은 Σ의 모든 순열의 집합이다.
1. a*b 역시 Sn의 원소이다.
2. (a*b)*c = a*(b*c) 이다.
3. 항등원이 존재한다.
4. 모든 순열에 대하여 역원이 존재한다.
하지만, a*b != b*a 이므로 아벨군은 아니다.
Find a^-1 mod m
만약 a와 m이 서로소라면 a^-1은 항상 존재한다.
확장 유클리드 알고리즘을 사용하면 a^-1을 구할 수 있는데, 확장 유클리드 알고리즘은 a와 b, 그의 최대공약수 gcd에 대해 gcd = ax+by를 만족하는 x와 y를 구한다. 이 때 x가 a^-1가 된다.
확장 유클리드 알고리즘은 다음과 같다.
int extended_gcd(int a, int b, int *x, int *y)
{
if (b == 0)
{
*x = 1;
*y = 0;
return a;
}
int x1 = *x;
int y1 = *y;
int gcd = extended_gcd(b, a % b, &x1, &y1);
*x = y1;
*y = x1 - (a / b) * y1;
return gcd;
}이름대로 기존의 유클리드 알고리즘을 응용하여 구현한다. gcd를 구하고, 구하는 과정을 역추적하며 x와 y를 계산한다.
b가 0이라면 gcd를 구한 것(a의 값)이고, 이 때의 x와 y는 각각 1, 0이다.
b * x1 + (a%b) * y1 = gcd(b, a%b)에서, a%b = a-b(a//b)이다. 따라서,
b* x1 + (a-b(a//b)) * y1
= b* x1 + a*y1 - b(a//b) * y1
= a*y1 -b(x1 - (a//b) * y1) = gcd(b, a%b)
이를 ax + by = gcd(a,b)꼴로 나타내려면,
x = y1
y = x1 - (a//b) * y1
이 된다.
이와 유사한 방식으로 모듈러 역원을 구하는 mul_inv 알고리즘 또한 구현할 수 있다.
만약 gcd가 1이라면 x가 a의 모듈러 역원 a^-1가 된다.
gcd가 1이 아니라면 역원은 존재하지 않는다.
갈루아 필드 GF(p)
galois field GF(p)는 소수 p에 대해 정의된 유한 필드이다. GF(p)는 0부터 p-1로 이루어진 집합이다. 이 집합의 산술 연산은 모듈러 p 연산을 따른다.
GF(11)은 {0,1,2,...,10}으로 이뤄져있고, 이 집합의 덧셈, 뺄셈, 곱셈 연산은 모두 mod 11로 수행된다.
이는 소수 p에 대해 정의된 유한 필드이므로 항상 곱셈에 대한 역원이 존재한다.
따라서 GF(p) 내의 산술연산은 잘 정돈되어 있으며(well-behaved) 덧셈 뺄셈 곱셈 나눗셈을 범위를 벗어나지 않고 수행할 수 있다.
예를 들어 선형 연립 방정식인
2x - y = 5 <= (1)
3x + 2y = 6 <= (2)
가 있다고 하자.
(1) * 2 + (2) 를 하면 y를 소거해 x를 구할 수 있을 것이다.
7x = 16 mod 11 = 5
x = 5 * 7^(-1) = 5 * 8 = 7
y는 x를 대입하여 구할 수 있다. => y = 9
만약 mod 2라면, 덧셈과 뺄셈은 XOR연산을 통해 수행된다.
0+0 = 0, 1+0 = 1, 0+1 = 1, 1+1 = 0이기 때문이다. 이를 통해 다항식 연산을 할 수 있다.
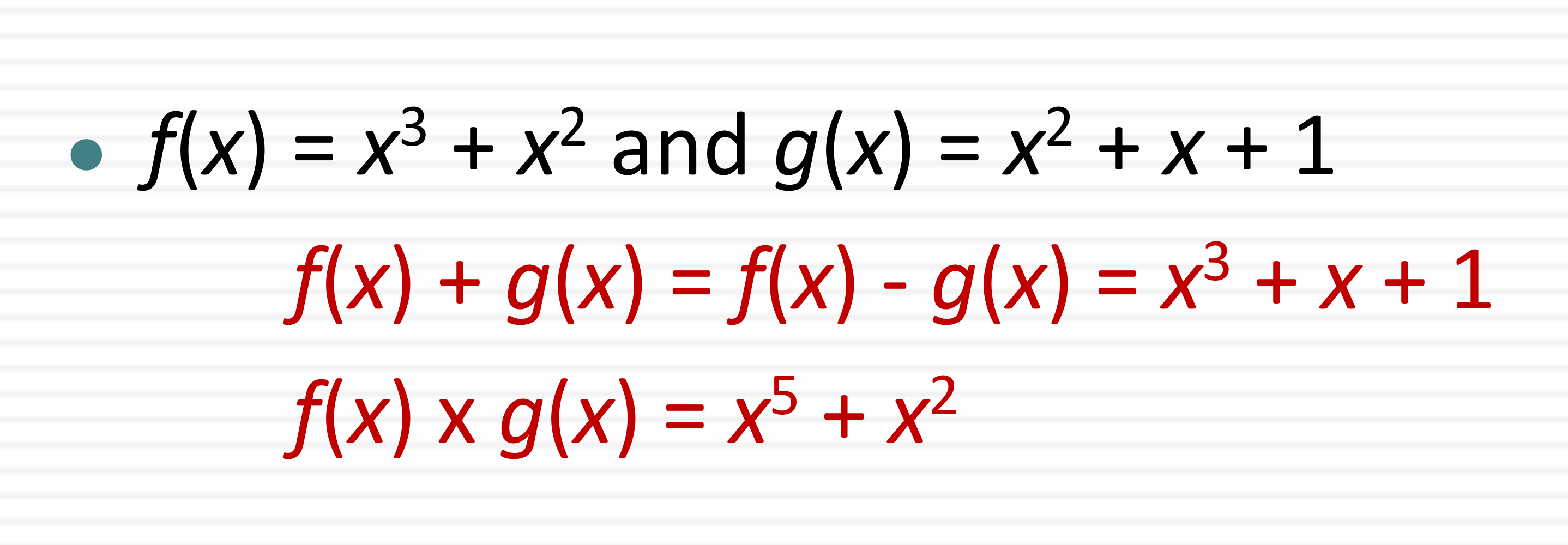
위와같은 연립방정식이 있을 때, 둘을 더함으로 x^3+x+1을 구해낼 수 있다. XOR연산이기 때문에 같은 차수를 더하면 소거되기 때문이다.
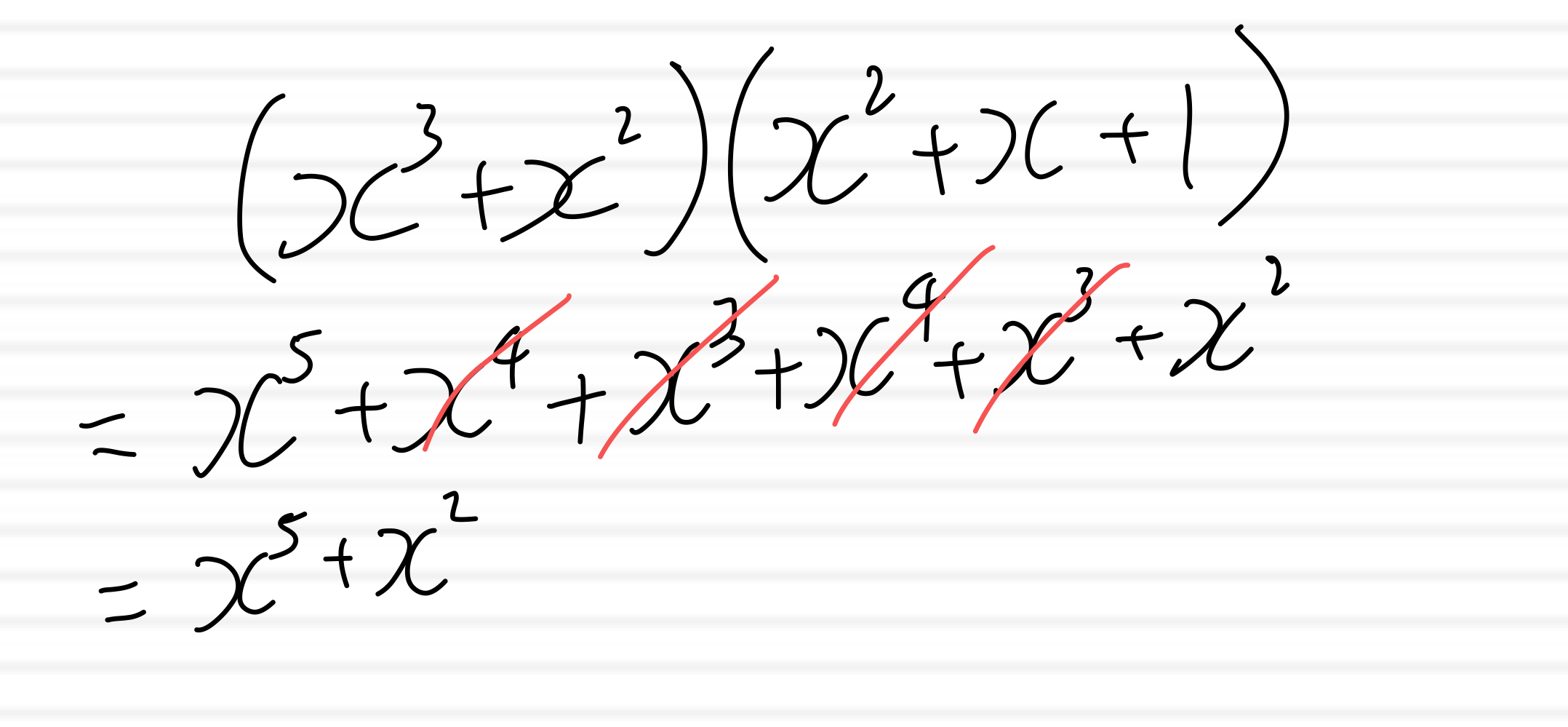
둘을 곱하면 x^5+x^2가 된다.
f(x) = q(x)g(x) + r(x)에서 r(x) = f(x) mod g(x)라고 할 때,
g(x)가 1이나 자기자신으로만 나누어 떨어진다면 g(x)를 irreducible(prime) polynomial(기약 다항식)이라 부른다.
GF(2^n)은, 차수가 n보다 작은 다항식으로 이뤄지며, 연산 이후 기약 다항식으로 나머지 연산을 취한다.
기약 다항식으로 나머지 연산을 취하므로 항상 역이 존재한다.

위 테이블은 GF(2^3)에서, 더하기 연산과 곱셈 연산의 결과를 정리한 것이다.
각 다항식은 바이너리로 나타낼 수 있다. 예를 들어 x^2+1은 101이다.

각 다항식을 10진수로 나타내면 위와 같다.
덧셈에서의 역은 자신이다. 곱셈에서의 역은 위 테이블에서 1이 되는 수로, (c)에 정리돼있다.
2x - 7y = 5 <= (1)
3x + 2y = 6 <= (2)
라는 연립방정식을 풀어보자.
(1) + (2)*6이라고 하자, 여기서 곱셈은 위 테이블을 참고한다.
2x - 7y = 5
+ 1x + 7y = 2
=> 3x = 7
x = 7 * 3^(-1) = 7 * 6 = 4
y는 위 식에 대입하여 구할 수 있다. => y = 5
덧셈, 곱셈, 나머지 연산은 XOR연산과 쉬프트 연산으로 할 수 있다.
더하기는 단순히 XOR연산을 통해 구현된다.
곱셈은 먼저 x 곱셈부터 구현하자.
uint8_t xtime(uint8_t x) {
return ((x<<1) ^ ((x>>7) & 1 ? 0x1B : 0));
}위 코드는 GF(2^8) mod x^8+x^4+x^3+x+1 에서의 x 곱셈 함수이다.
x를 곱한다는 것은 각 자리에서 1만큼 왼쪽 쉬프트를 하는 것을 뜻한다.
만약 x가 8bit를 넘어간다면 나머지 연산을 위해 x^4+x^3+x+1을 더해준다.
uint8_t Multiply(uint8_t a, uinit8_t b) {
uint8_t r = 0;
while (b > 0) {
if (b & 1) r = r ^ a;
b = b >> 1;
a = xtime(a);
}
return r;
}위 함수는 xtime 함수를 사용하여 곱셈을 구현한다. 구현 방식은 일반적인 곱셈 방법처럼,
r에는 곱셈의 결과값을 저장한다. b를 가장 낮은 차수인 가장 오른쪽 비트에서부터 왼쪽으로 순회한다. 이는 b=b>>1로 구현되어있다.
만약 현재 순회중인 차수가 존재한다면 (b&1 == 1)이라면, r에 현재 a를 더해준다. 이때 a는 각 차수에 알맞게 곱해져있는 상태이다. 이는 a = xtime(a)로 구현되어있다.
b의 순회가 끝나면 곱셈의 결과가 나온다.
'학교강의필기장 > 암호학' 카테고리의 다른 글
| 5. Random Number (2) | 2023.10.16 |
|---|---|
| 4. DES, block/stream cipher mode (0) | 2023.10.15 |
| 3. AES (0) | 2023.10.12 |
| 1. 고전 암호화 기법들 (0) | 2023.09.07 |
| 0. 암호학 개요 (0) | 2023.09.04 |
