Syntactic Sugar
구문 설탕은 언어의 표현력을 증가시키진 않지만 프로그램을 더 읽고 쓰기 편하게 만들어준다.
예를 들어, let x = E1 in E2도 사실 설탕에 속하는데, 여기서 설탕을 빼면 (proc x E2) E1이 된다.
let x = 1 in
let y = 2 in
x + y위와 같은 구문이,
=> (proc (x) (let y = 2 in x + y)) 1
=> (proc (x) ((proc (y) (x + y)) 2)) 1설탕이 빠지면 이렇게 난잡해진다.
즉 우리가 사용한 기존 문법에서,
let x = E1 in E2 ⇒ (proc (x) E2) E1 로 설탕을 쳐낼 수 있고
letrec f(x) = E1 in E2 ⇒ let f = proc (x) (E1) in E2 으로 설탕을 쳐낼 수 있다.
모든 구문 설탕을 제거하면 람다 대수를 얻을 수 있다.
Lambda Calculus
람다 대수는 구문 설탕 없이 최소한의 언어를 구성한다.
함수가 λ-computable하다면 이는 turing computable하다.
e → x # 변수
| λx.e # 추상화
| e e # 적용
⇒ 적용은 왼쪽으로 결합한다. 예를 들어서 s t u 인 경우, (s t) u로 연산한다.
⇒ 추상화의 본체는 가능한 한 멀리 오른쪽으로 확장된다. λx.λy.x y x는 λx.(λy.((x y) x)) 로 연산한다.
Bound and Free Variables
λy.(x y) 에서, y는 bound 변수, x는 free 변수이다.
λz. λx. λx. (y z) 에서, y는 free 변수이다.
자유 변수가 없는 표현식을 closed expressions, 닫힌 표현식 또는 combinators, 조합자라고 한다.
Evaluation
람다 대수 표현식을 평가하기 위해서는 β 축약(β-reduction)이라는 과정을 반복해야한다.
1. Redex(축약 가능 표현식) 찾기 : (λx.e1) e2 형태의 부분 표현식을 찾는다.
2. β-축약 수행 : (λx.e1) e2를 e1에서 모든 x를 e2로 대체하여 다시 쓴다. 즉, (λx.e1) e2 = [x ↦ e2] e1 이다.
위 과정을 Redex가 없을 때까지 반복한다.
예를 들어, (λx.(λy.x)) z 가 있다고 하자.
- 표현식 (λx.(λy.x)) z 는 redex이다. 따라서 [x ↦ z](λy.x) 가 된다. x의 모든 발생을 z로 대체하므로, λy.z가 된다.
다시, (λx.(λy.x y)) (λx.x) z가 있다고 하자.
- 표현식 λy.x y는 redex이다. [y ↦ y] x 이므로, x가 된다. ⇒ (λx.x) (λx.x) z
- 표현식 (λx.x) z는 redex이다. [x ↦ z] x 이므로, z가 된다. ⇒ (λx.x) z
- 같은 이유로 이 표현식은 z가 된다.
Substitution
[x ↦ e1] e2에서,
[x ↦ e1] x 라면, x를 e1으로 치환한다.
[x ↦ e1] y 라면, y는 그대로 남는다.
[x ↦ e1](λy.e2) 라면, λz.[x ↦ e1]([y ↦ z] e2) 이다.
- 여기서 알파 변환을 수행하는 이유는 e2에서 y가 쓰일 때, 변수 바인딩과 범위를 고려하기 위해서이다.
[x ↦ e1](e2 e3) 라면, ([x ↦ e1]e2 [x ↦ e1]e3) 이다.
Evaluation Strategy - Normal Order
정규 순서는 가장 왼쪽에 있는 바깥쪽의 redex를 가장 먼저 축약하는 평가 전략이다.
이 전략은 항상 적절한 경우 결과를 도출할 수 있고, 평가 순서가 결정론적이다.

여기서 Id는 λx.x를 의미한다.
Evaluation Strategy - Call-by-name
Call-by-name 전략은 정규 순서와 비슷하지만, 람다 추상화 내부에서는 축약을 허용하지 않는다.
이 전략은 lazy 평가 전략으로 실제로 사용되는 인자만 평가한다.
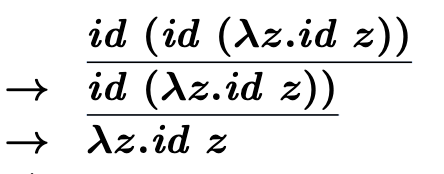
Evaluation Strategy - Call-by-value
Call-by-value 전략은 가장 바깥쪽 redex 중 오른쪽 부분의 redex를 먼저 축약하는 평가 전략이다. 이 전략은 엄격(strict) 평가 전략으로, 함수의 본문에서 사용 여부와 관계없이 인자를 항상 평가한다.

Compiling to Lambda Calculus
표현식 e는 컴파일 과정에서 람다 계산식으로 변환된다.
기본 값 변환

여기서, s^n은 s를 n번 적용한 것을 의미한다.
'학교강의필기장 > 프로그래밍언어론' 카테고리의 다른 글
| 11. Let-Polymorphic Type System (0) | 2024.06.19 |
|---|---|
| 10. Automatic Type Inference (0) | 2024.06.19 |
| 9. Type System (0) | 2024.06.19 |
| 8. 레코드, 포인터, 메모리 관리(수동, 가비지컬렉션) (0) | 2024.06.19 |
| 7. 명시적 참조 & 암시적 참조 (0) | 2024.06.19 |
