Motivation
현재까지, 문법과 의미를 엄밀하게 정의하고 정식 설계를 반영한 인터프리터를 구현함으로써 Program → Interpreter → Result 구조의 언어를 설계하였다.
그러나 현재 시스템에는 안전하지 않은 프로그램을 실행하려 시도하여 런타임 에러가 발생할 수 있다. (C++, Python, JS 등의 언어가 그렇다)
따라서 프로그램의 안전성을 분석하고 모든 버그를 정적으로 탐지하는 자동화된 기술을 만들어야 한다.
Program → Analyzer → Interpreter → Result
Static Analyzer는 정적, 그리고 자동으로 소프트웨어 버그를 감지한다.
static: 실행 전에 프로그램 텍스트를 분석한다.
automatic: Static Analyzer로 sw를 분석한다.
이는 불결정성(impurity) 문제를 가지고 있다. 즉 완전(completeness)하고 정확(soundness)한 정적 분석은 불가능하다. 하지만 근사적이면서도 유용한 정적 분석은 가능하다.
Soundness: 프로그램에 오류가 있으면 분석기는 프로그램을 거부한다. 모든 안전하지 않은 프로그램은 거부된다. 즉 False Negative가 없다.
Completeness: 분석기가 프로그램을 거부하면 그 프로그램에는 오류가 있다. 모든 안전한 프로그램은 수용된다. 즉 False Positive가 없다.
우리는 정확하지만 완전하지 않은 타입 시스템을 사용할 것이다. 즉, 모든 타입 오류를 감지한다.
Type
T → int
| bool
| T → T
여기서, T → T는 변수에서 타입으로의 매핑을 나타낸다.
이를 Γ ⊢ e : t 로 표기하고, 표현식 e가 타입 t를 가진다는 뜻이다.
Typing Rules
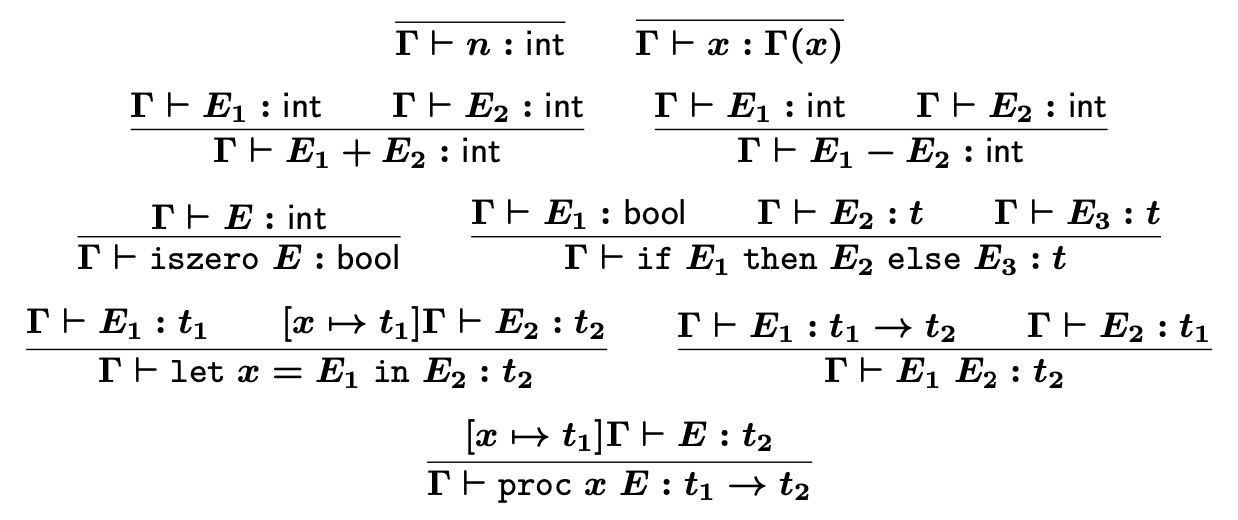
[] ⊢ E : t는 닫힌 표현식 E가 타입 t를 가지는 조건이다.
Multiple Types
proc x x위 함수의 경우 다양한 타입을 가질 수 있다.
예를 들어, [x ↦ int] ⊢ x : int 이고, [x ↦ bool] ⊢ x : bool이다.
Soundness
타입 시스템이 정확하다는 것은,
만약 닫힌 표현식 E가 [] ↦ E : t, 즉 잘 타입되어 있다면
[] ⊢ E ⇒ v, E는 타입 오류가 없고 값을 생성한다. 또 값 v의 타입은 t이다.
만약 E에 타입 오류가 있다면 E에 대해 [] ⊢ E : t인 t를 찾을 수 없다.
즉, 닫힌 표현식 E에 대해, [] ⊢ E : t ⇒ [] ⊢ E ⇒ v 이며, v:t 임을 증명할 수 있다.
Proof.
Case E = n: [] ⊢ E : int, [] ⊢ E ⇒ n 에서 n : int이므로 정리가 성립한다.
Case E = x: 이는 닫힌 표현식이 아니다.
Case E = E1 + E2: [] ⊢ E : int ⇒ [] ⊢ E ⇒ n을 어떤 정수 n에 대해 보인다.
- IH : 어떤 정수 n1과 n2에 대하여 [] ⊢ E1 : int ⇒ [] ⊢ E1 ⇒ n1 이고, [] ⊢ E2 : int ⇒ [] ⊢ E2 ⇒ n2 이다.
만약, [] ⊢ E1 + E2 : int 라면, [] ⊢ E1 : int 이고 [] ⊢ E2 : int이다.
IH에서, [] ⊢ E1 ⇒ n1 이고, [] ⊢ E2 ⇒ n2 이다.
따라서, 평가 규칙(evaluation rules)에 따라 [] ⊢ E1 + E2 ⇒ n1 + n2이다.
Incompleteness
타입 시스템은 불완전하다. 즉, 어떤 프로그램이 타입 오류가 없더라도 타입 시스템에 의해 타입을 가지지 않을 수 있다.
(if E then 1 else (true)) + 1여기서 E의 평가 결과를 미리 알 수 있다면 E가 true인지 false인지 종료되지 않는지를 알 수 있지만, 이는 불가능하다.
실행 없이 모든 가능한 값을 정확히 계산할 수 없다. 이는 엘런 튜링에 의해 증명되었다. (halting problem)
Implementation
type을 검사하는데에는 두 가지 접근법이 있다.
Type Annotation(타입 주석): 프로그래머가 함수 인자의 타입을 제공한다. (C, C++, Java...)
Type Inference(타입 추론): 타입 검사기가 자동으로 타입을 추론한다. 언어가 신중하게 설계되어 있을 때 가능하다.
Example
[] ⊢ proc (x: int) (x+1)의 타입을 추론한다고 하자.
Γ = [], 초기 타입 환경 Γ는 비어 있다.
Γ' ⊢ x : int, x는 int로 주어졌다. x의 타입을 int로 타입 환경에 추가한다.
새로운 타입 환경 Γ' = [x ↦ int]를 사용하여 본문 (x+1)의 타입을 검사한다.
Γ' ⊢ x : int
Γ' ⊢ 1 : int
Γ' ⊢ x + 1 : int
따라서,
[x ↦ int] ⊢ x + 1 : int ⇒ Γ ⊢ proc (x : int) (x + 1) : int → int 이다.
Type Check Algorithm
우리는 type checking algorithm을 재귀적으로 구현할 수 있다.
let rec typeof gamma E =
match E with
| proc (x : t1) E1 ->
let new_env = (x : t1) :: env in
let t2 = typeof new_env E1 in
TFunc (t, t2) (* t -> t2 *)
| ...위와 같은 방식으로 구현 된다.
'학교강의필기장 > 프로그래밍언어론' 카테고리의 다른 글
| 11. Let-Polymorphic Type System (0) | 2024.06.19 |
|---|---|
| 10. Automatic Type Inference (0) | 2024.06.19 |
| 8. 레코드, 포인터, 메모리 관리(수동, 가비지컬렉션) (0) | 2024.06.19 |
| 7. 명시적 참조 & 암시적 참조 (0) | 2024.06.19 |
| 6. 간단한 언어 만들어보기 - 2 (1) | 2024.04.21 |
Motivation
현재까지, 문법과 의미를 엄밀하게 정의하고 정식 설계를 반영한 인터프리터를 구현함으로써 Program → Interpreter → Result 구조의 언어를 설계하였다.
그러나 현재 시스템에는 안전하지 않은 프로그램을 실행하려 시도하여 런타임 에러가 발생할 수 있다. (C++, Python, JS 등의 언어가 그렇다)
따라서 프로그램의 안전성을 분석하고 모든 버그를 정적으로 탐지하는 자동화된 기술을 만들어야 한다.
Program → Analyzer → Interpreter → Result
Static Analyzer는 정적, 그리고 자동으로 소프트웨어 버그를 감지한다.
static: 실행 전에 프로그램 텍스트를 분석한다.
automatic: Static Analyzer로 sw를 분석한다.
이는 불결정성(impurity) 문제를 가지고 있다. 즉 완전(completeness)하고 정확(soundness)한 정적 분석은 불가능하다. 하지만 근사적이면서도 유용한 정적 분석은 가능하다.
Soundness: 프로그램에 오류가 있으면 분석기는 프로그램을 거부한다. 모든 안전하지 않은 프로그램은 거부된다. 즉 False Negative가 없다.
Completeness: 분석기가 프로그램을 거부하면 그 프로그램에는 오류가 있다. 모든 안전한 프로그램은 수용된다. 즉 False Positive가 없다.
우리는 정확하지만 완전하지 않은 타입 시스템을 사용할 것이다. 즉, 모든 타입 오류를 감지한다.
Type
T → int
| bool
| T → T
여기서, T → T는 변수에서 타입으로의 매핑을 나타낸다.
이를 Γ ⊢ e : t 로 표기하고, 표현식 e가 타입 t를 가진다는 뜻이다.
Typing Rules
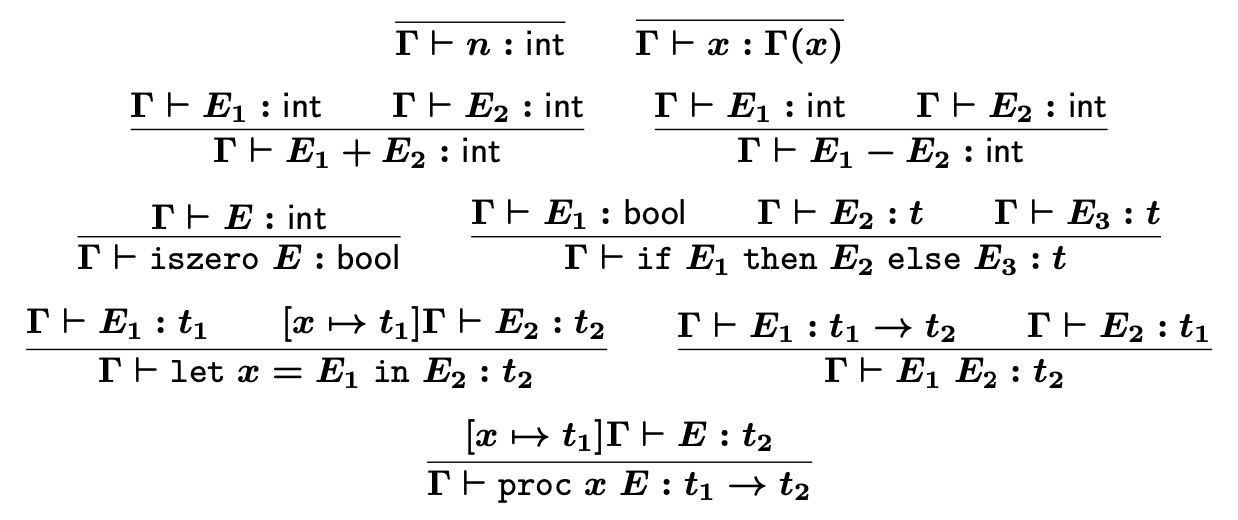
[] ⊢ E : t는 닫힌 표현식 E가 타입 t를 가지는 조건이다.
Multiple Types
proc x x위 함수의 경우 다양한 타입을 가질 수 있다.
예를 들어, [x ↦ int] ⊢ x : int 이고, [x ↦ bool] ⊢ x : bool이다.
Soundness
타입 시스템이 정확하다는 것은,
만약 닫힌 표현식 E가 [] ↦ E : t, 즉 잘 타입되어 있다면
[] ⊢ E ⇒ v, E는 타입 오류가 없고 값을 생성한다. 또 값 v의 타입은 t이다.
만약 E에 타입 오류가 있다면 E에 대해 [] ⊢ E : t인 t를 찾을 수 없다.
즉, 닫힌 표현식 E에 대해, [] ⊢ E : t ⇒ [] ⊢ E ⇒ v 이며, v:t 임을 증명할 수 있다.
Proof.
Case E = n: [] ⊢ E : int, [] ⊢ E ⇒ n 에서 n : int이므로 정리가 성립한다.
Case E = x: 이는 닫힌 표현식이 아니다.
Case E = E1 + E2: [] ⊢ E : int ⇒ [] ⊢ E ⇒ n을 어떤 정수 n에 대해 보인다.
- IH : 어떤 정수 n1과 n2에 대하여 [] ⊢ E1 : int ⇒ [] ⊢ E1 ⇒ n1 이고, [] ⊢ E2 : int ⇒ [] ⊢ E2 ⇒ n2 이다.
만약, [] ⊢ E1 + E2 : int 라면, [] ⊢ E1 : int 이고 [] ⊢ E2 : int이다.
IH에서, [] ⊢ E1 ⇒ n1 이고, [] ⊢ E2 ⇒ n2 이다.
따라서, 평가 규칙(evaluation rules)에 따라 [] ⊢ E1 + E2 ⇒ n1 + n2이다.
Incompleteness
타입 시스템은 불완전하다. 즉, 어떤 프로그램이 타입 오류가 없더라도 타입 시스템에 의해 타입을 가지지 않을 수 있다.
(if E then 1 else (true)) + 1여기서 E의 평가 결과를 미리 알 수 있다면 E가 true인지 false인지 종료되지 않는지를 알 수 있지만, 이는 불가능하다.
실행 없이 모든 가능한 값을 정확히 계산할 수 없다. 이는 엘런 튜링에 의해 증명되었다. (halting problem)
Implementation
type을 검사하는데에는 두 가지 접근법이 있다.
Type Annotation(타입 주석): 프로그래머가 함수 인자의 타입을 제공한다. (C, C++, Java...)
Type Inference(타입 추론): 타입 검사기가 자동으로 타입을 추론한다. 언어가 신중하게 설계되어 있을 때 가능하다.
Example
[] ⊢ proc (x: int) (x+1)의 타입을 추론한다고 하자.
Γ = [], 초기 타입 환경 Γ는 비어 있다.
Γ' ⊢ x : int, x는 int로 주어졌다. x의 타입을 int로 타입 환경에 추가한다.
새로운 타입 환경 Γ' = [x ↦ int]를 사용하여 본문 (x+1)의 타입을 검사한다.
Γ' ⊢ x : int
Γ' ⊢ 1 : int
Γ' ⊢ x + 1 : int
따라서,
[x ↦ int] ⊢ x + 1 : int ⇒ Γ ⊢ proc (x : int) (x + 1) : int → int 이다.
Type Check Algorithm
우리는 type checking algorithm을 재귀적으로 구현할 수 있다.
let rec typeof gamma E =
match E with
| proc (x : t1) E1 ->
let new_env = (x : t1) :: env in
let t2 = typeof new_env E1 in
TFunc (t, t2) (* t -> t2 *)
| ...위와 같은 방식으로 구현 된다.
'학교강의필기장 > 프로그래밍언어론' 카테고리의 다른 글
| 11. Let-Polymorphic Type System (0) | 2024.06.19 |
|---|---|
| 10. Automatic Type Inference (0) | 2024.06.19 |
| 8. 레코드, 포인터, 메모리 관리(수동, 가비지컬렉션) (0) | 2024.06.19 |
| 7. 명시적 참조 & 암시적 참조 (0) | 2024.06.19 |
| 6. 간단한 언어 만들어보기 - 2 (1) | 2024.04.21 |
