Let-Polymorphic Type Checking Algorithm
let 다형성을 지원하는 타입 체크 알고리즘은 재계산을 피하고 효율적으로 타입 체크를 수행하기 위해 더 정교한 알고리즘을 사용한다.
1. Γ라는 타입 환경에서 표현식 e1을 찾기 위해 일반적인 타입 체크 알고리즘을 사용한다. (U(V(Γ, e1, t)))
2. 타입 일반화: 타입 t에서 남아있는 변수를 일반화해서 type scheme, ∀α1 ... α_n.t 을 구한다. 이들은 t에서 나타나는 타입 변수들이다.
3. 바인드된 변수 x에 대해 타입 스킴을 기록하도록 타입 환경을 확장하고, e2에 대해 타입 체크를 시작한다.
4. x의 각 발생마다 새로운 타입 변수 β1 ... β_n을 생성하고 이를 사용하여 타입 스킴을 인스턴스화 한다.

위와 같은 표현식과 타입 방정식이 있다고 하자. 우리는 proc (x) 1 에 대한 다형성을 처리할 것이다.
먼저 proc (x) 1 에 대한 타입 방정식을 구한다. 이는 t_x → int로 구해진다.
이렇게 구한 타입 t4, t_x → int에서 남은 변수인 t_x를 일반화하여 type scheme를 구한다. 이는 t_f = ∀t_x . t_x → int로 표현된다.
이 t_x가 발생할 때마다 새로운 타입 변수 β를 생성하여 타입 스킴을 인스턴스화 할 것이다.

먼저 여기까지 unification algorithm을 통해 구한다.

다음, t_f에 대입할 때 t_x가 발생한다. 이는 β1을 생성 및 사용하여 인스턴스화 한다.
위 방정식을 단순화 하면, β1 = int ∧ int = t2가 된다.

다음 다시 t_f에 대입할 때 t_x가 발생한다. β2를 생성 및 사용하여 인스턴스화 한다.
위 방정식을 단순화 하면, β2 = bool ∧ int = t3가 된다.
기존 타입 환경 변수 일반화X
기존 타입 환경에 있던 변수들에 대해서는 일반화를 진행하지 않는다.
만약 기존 타입 환경에 있는 변수들까지 일반화를 진행하면 어떻게 될까?
기존 타입 환경 변수 일반화 진행

위와 같은 표현식과 타입 방정식이 있다고 하자.
이는 t1 : proc (x) c = t_x → t_c 에 대한 다형성을 구하고자 한다.
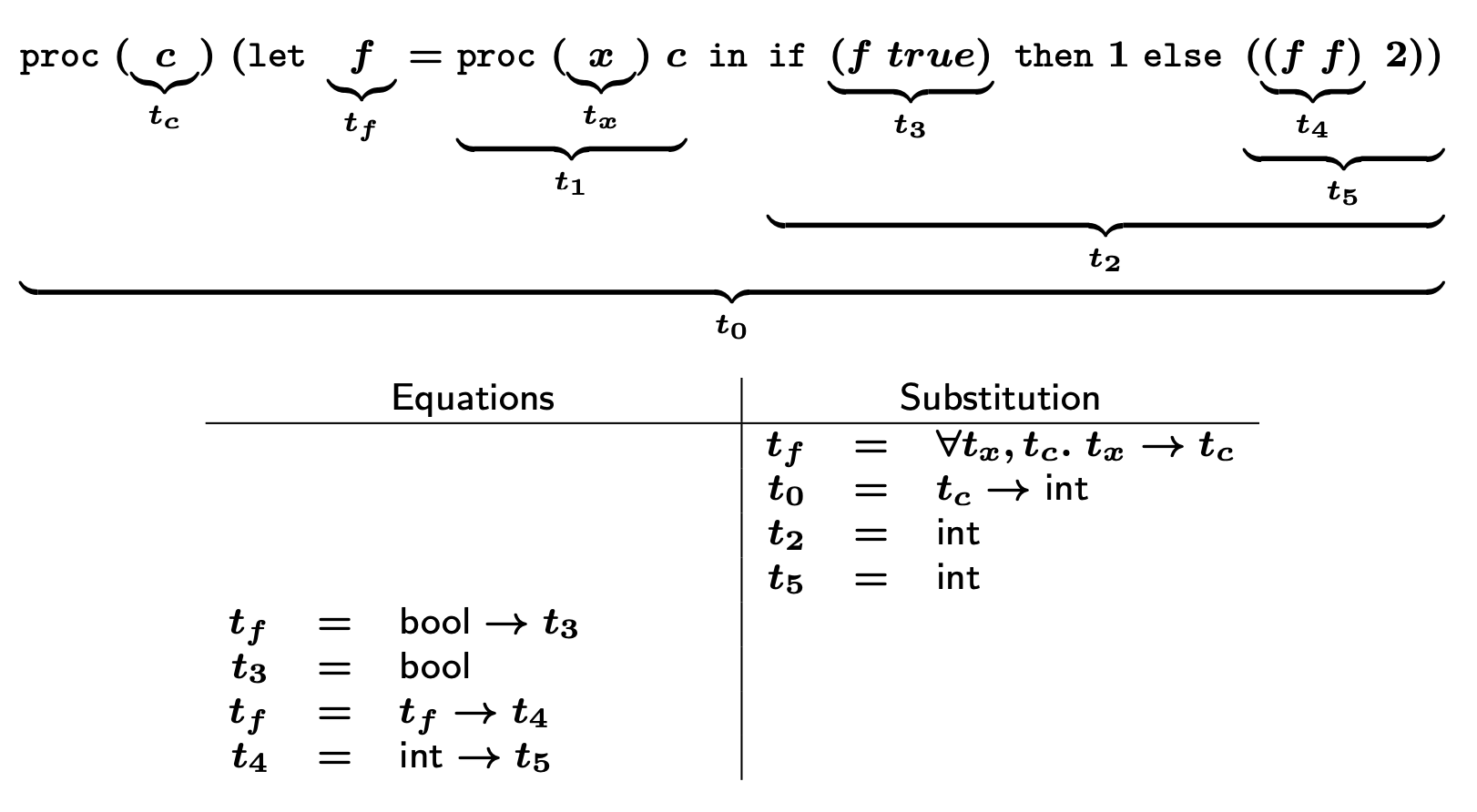
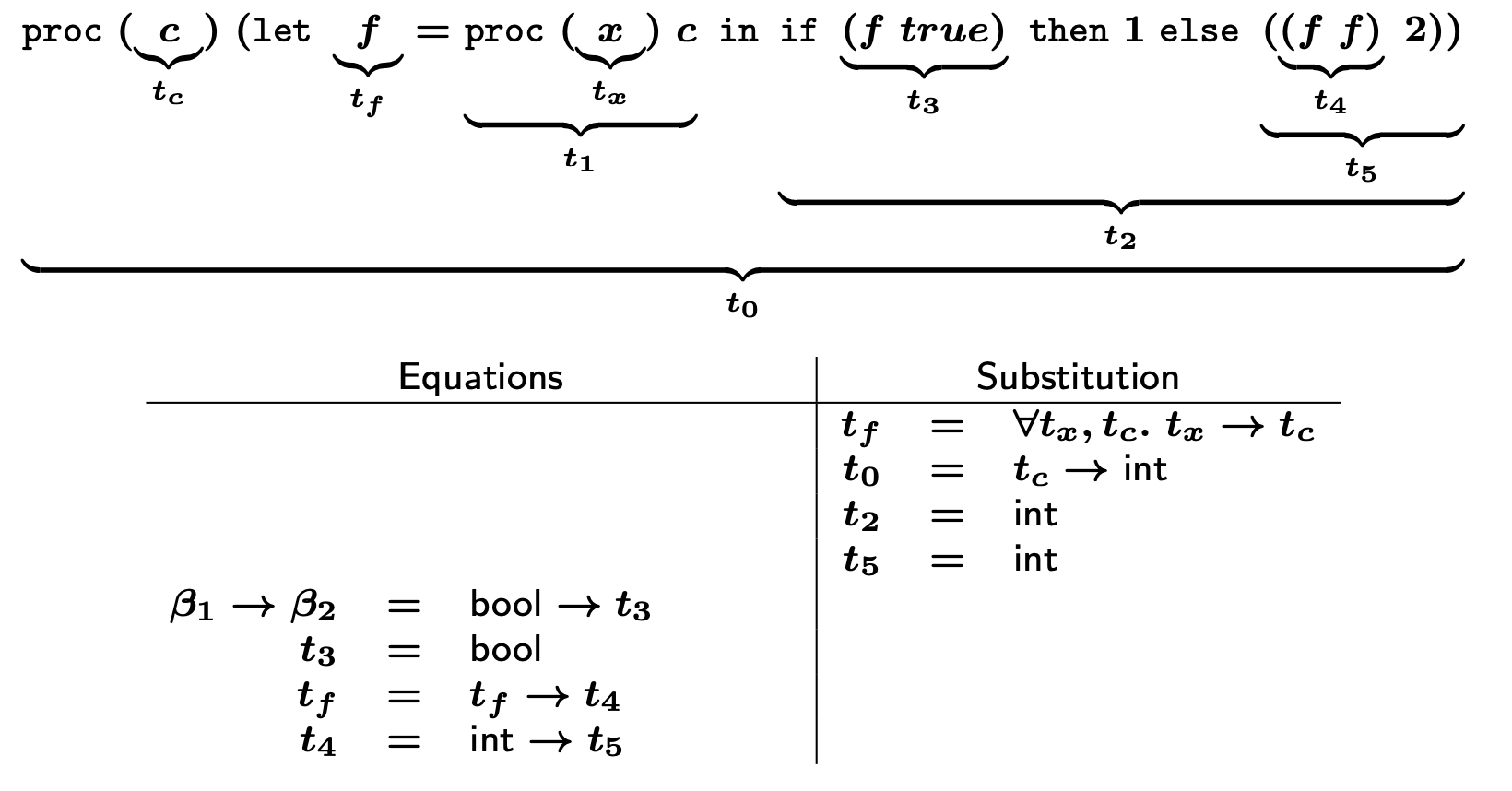
t_f는 β1 → β2로 대입된다. 따라서 β1 = bool ∧ β2 = t3 (t3 = bool)가 된다.
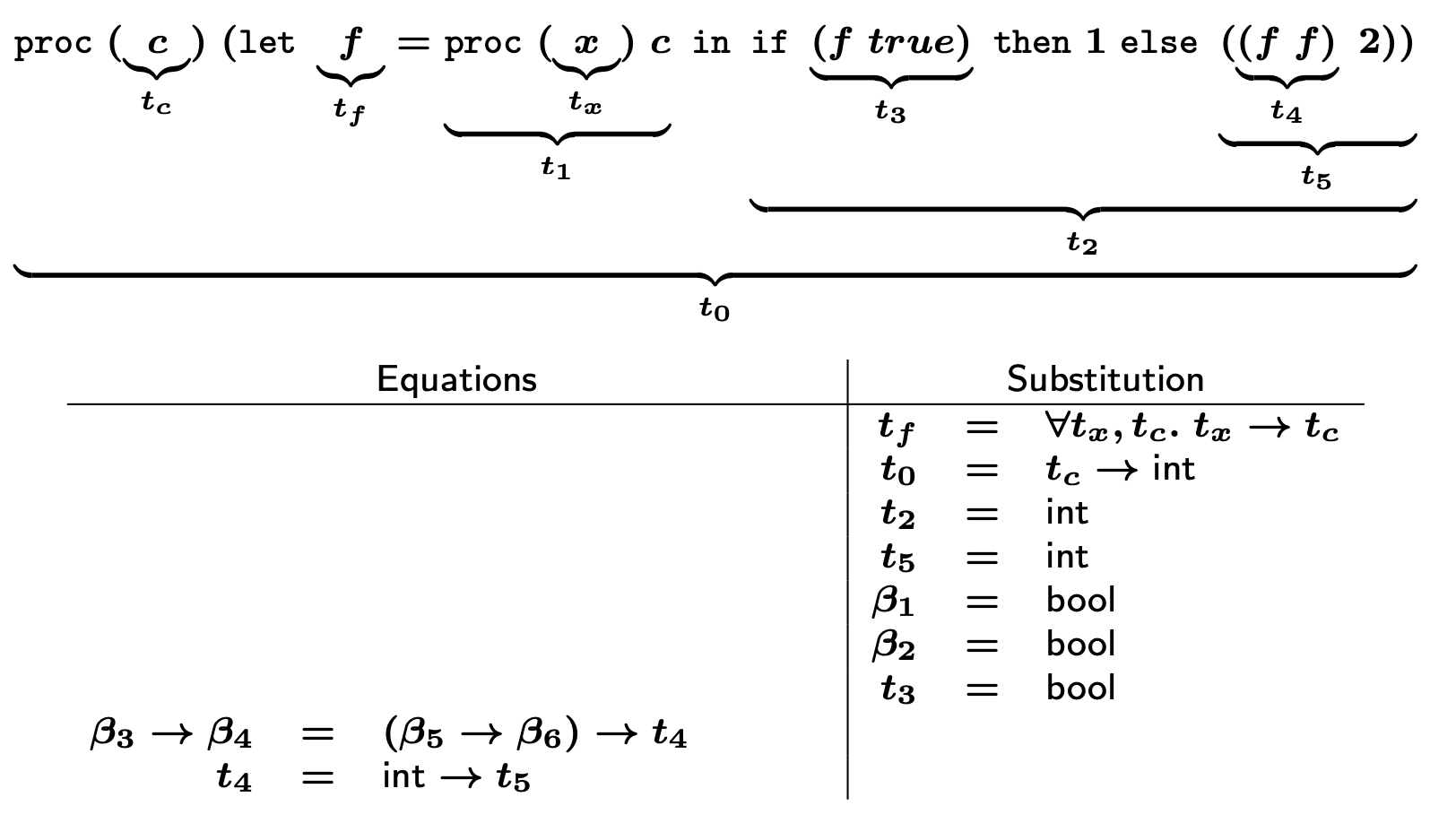
마찬가지로 t_f는 β3 → β4, 우항의 t_f는 β5 → β6으로 대입된다.
따라서 β3 = (β5 → β6) ^ β4 → t4 (t4 = int → int)가 된다.
그런데 여기서, c가 β2에서는 bool로 쓰이고, β4에서는 (int → int)로 쓰인다. c는 bool과 프로시저로 동시에 존재할 수 없다.
따라서 기존 타입 환경 변수는 일반화를 진행하지 않는다.
기존 타입 환경 변수 일반화 X
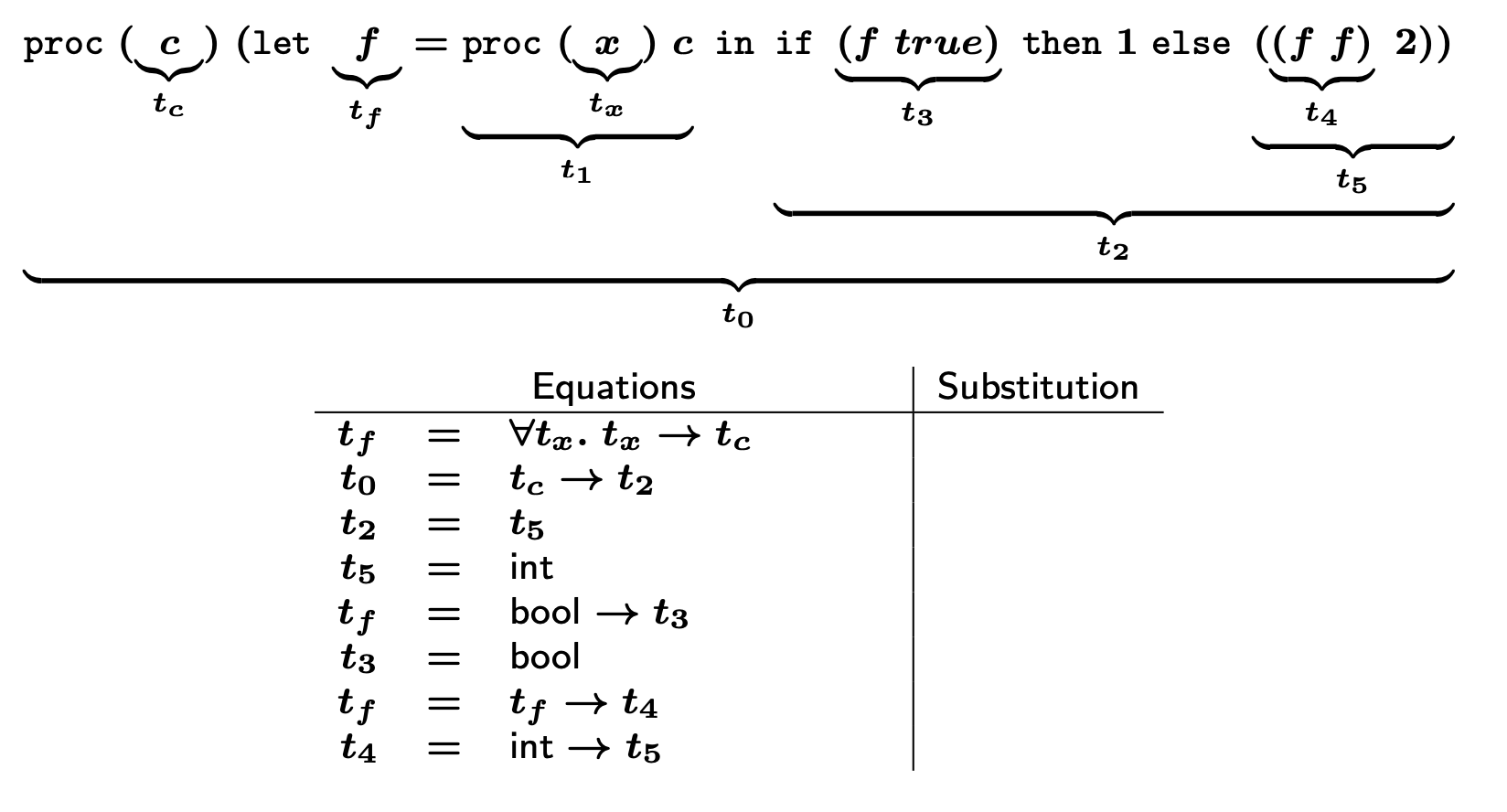
c에 대한 일반화를 진행하지 않으므로, t_f = ∀t_x.t_x → t_c이다.
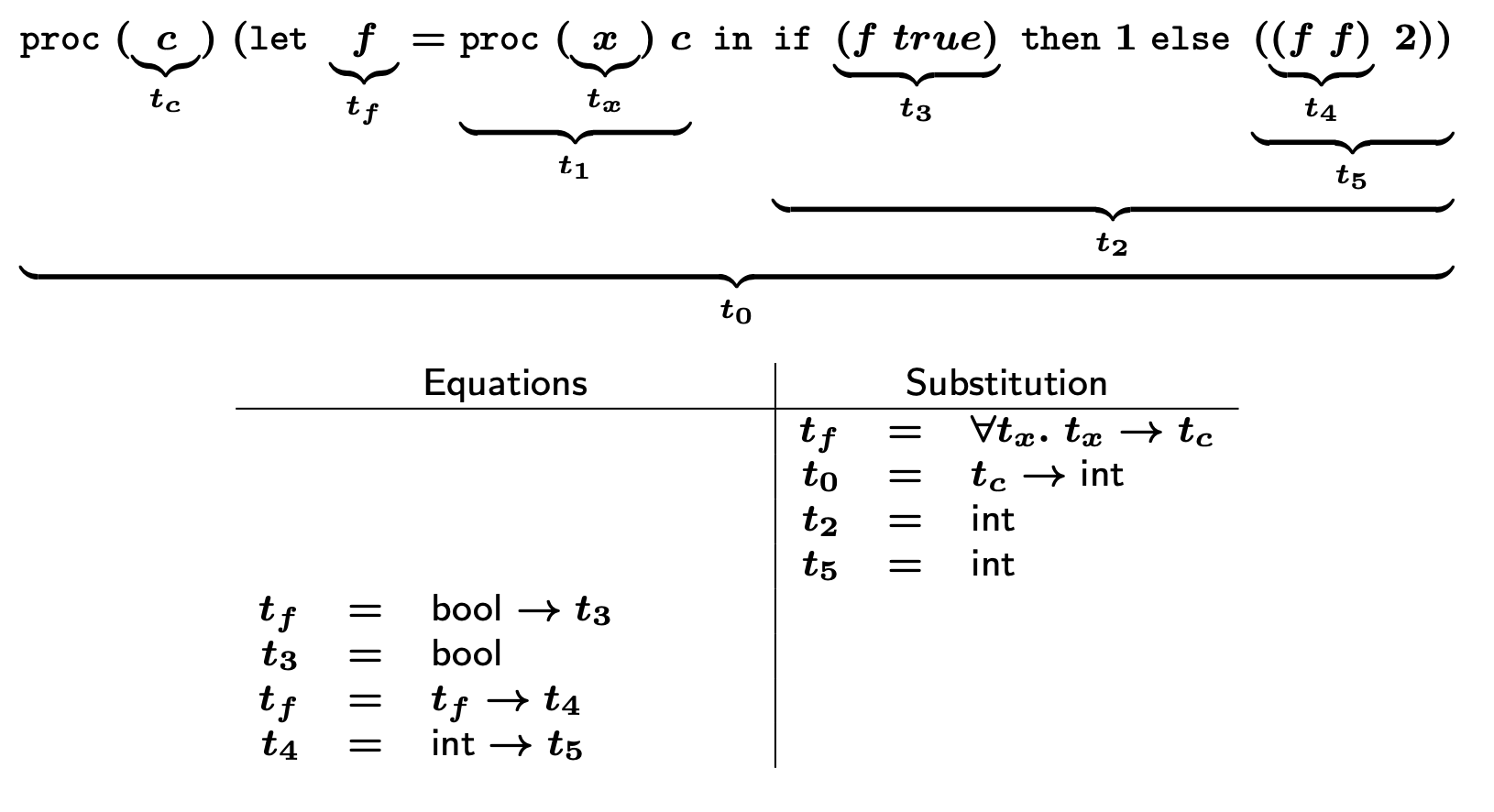
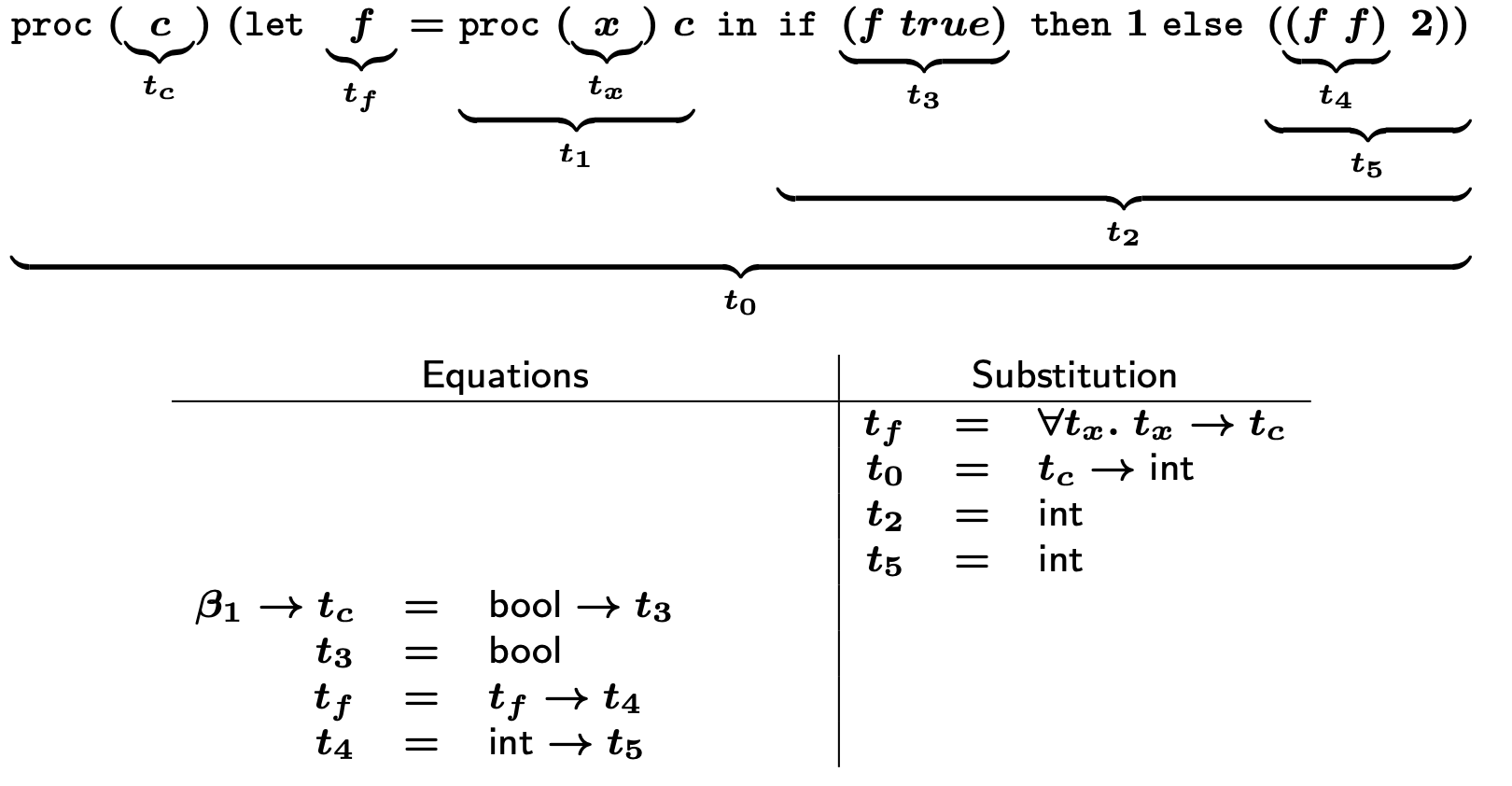
t_f는 β1 → t_c로 대입된다. 따라서 β1 = bool ∧ t_c = t3 (t3 = bool)이 된다.

다시, t_f는 β2 → t_c로 대입되고 우항의 t_f는 β3 → t_c로 대입된다.
t_c는 bool이므로 β2 = (β3 → bool) ∧ bool = t4가 되는데, 여기서 t4 = bool이 되었으므로
추후 t4 = int → t5에서 bool = int → int라는 모순이 생겨 에러가 발생한다.
'학교강의필기장 > 프로그래밍언어론' 카테고리의 다른 글
| 12. Lambda Calculus (0) | 2024.06.19 |
|---|---|
| 10. Automatic Type Inference (0) | 2024.06.19 |
| 9. Type System (0) | 2024.06.19 |
| 8. 레코드, 포인터, 메모리 관리(수동, 가비지컬렉션) (0) | 2024.06.19 |
| 7. 명시적 참조 & 암시적 참조 (0) | 2024.06.19 |
Let-Polymorphic Type Checking Algorithm
let 다형성을 지원하는 타입 체크 알고리즘은 재계산을 피하고 효율적으로 타입 체크를 수행하기 위해 더 정교한 알고리즘을 사용한다.
1. Γ라는 타입 환경에서 표현식 e1을 찾기 위해 일반적인 타입 체크 알고리즘을 사용한다. (U(V(Γ, e1, t)))
2. 타입 일반화: 타입 t에서 남아있는 변수를 일반화해서 type scheme, ∀α1 ... α_n.t 을 구한다. 이들은 t에서 나타나는 타입 변수들이다.
3. 바인드된 변수 x에 대해 타입 스킴을 기록하도록 타입 환경을 확장하고, e2에 대해 타입 체크를 시작한다.
4. x의 각 발생마다 새로운 타입 변수 β1 ... β_n을 생성하고 이를 사용하여 타입 스킴을 인스턴스화 한다.

위와 같은 표현식과 타입 방정식이 있다고 하자. 우리는 proc (x) 1 에 대한 다형성을 처리할 것이다.
먼저 proc (x) 1 에 대한 타입 방정식을 구한다. 이는 t_x → int로 구해진다.
이렇게 구한 타입 t4, t_x → int에서 남은 변수인 t_x를 일반화하여 type scheme를 구한다. 이는 t_f = ∀t_x . t_x → int로 표현된다.
이 t_x가 발생할 때마다 새로운 타입 변수 β를 생성하여 타입 스킴을 인스턴스화 할 것이다.

먼저 여기까지 unification algorithm을 통해 구한다.

다음, t_f에 대입할 때 t_x가 발생한다. 이는 β1을 생성 및 사용하여 인스턴스화 한다.
위 방정식을 단순화 하면, β1 = int ∧ int = t2가 된다.

다음 다시 t_f에 대입할 때 t_x가 발생한다. β2를 생성 및 사용하여 인스턴스화 한다.
위 방정식을 단순화 하면, β2 = bool ∧ int = t3가 된다.
기존 타입 환경 변수 일반화X
기존 타입 환경에 있던 변수들에 대해서는 일반화를 진행하지 않는다.
만약 기존 타입 환경에 있는 변수들까지 일반화를 진행하면 어떻게 될까?
기존 타입 환경 변수 일반화 진행

위와 같은 표현식과 타입 방정식이 있다고 하자.
이는 t1 : proc (x) c = t_x → t_c 에 대한 다형성을 구하고자 한다.


t_f는 β1 → β2로 대입된다. 따라서 β1 = bool ∧ β2 = t3 (t3 = bool)가 된다.

마찬가지로 t_f는 β3 → β4, 우항의 t_f는 β5 → β6으로 대입된다.
따라서 β3 = (β5 → β6) ^ β4 → t4 (t4 = int → int)가 된다.
그런데 여기서, c가 β2에서는 bool로 쓰이고, β4에서는 (int → int)로 쓰인다. c는 bool과 프로시저로 동시에 존재할 수 없다.
따라서 기존 타입 환경 변수는 일반화를 진행하지 않는다.
기존 타입 환경 변수 일반화 X

c에 대한 일반화를 진행하지 않으므로, t_f = ∀t_x.t_x → t_c이다.


t_f는 β1 → t_c로 대입된다. 따라서 β1 = bool ∧ t_c = t3 (t3 = bool)이 된다.

다시, t_f는 β2 → t_c로 대입되고 우항의 t_f는 β3 → t_c로 대입된다.
t_c는 bool이므로 β2 = (β3 → bool) ∧ bool = t4가 되는데, 여기서 t4 = bool이 되었으므로
추후 t4 = int → t5에서 bool = int → int라는 모순이 생겨 에러가 발생한다.
'학교강의필기장 > 프로그래밍언어론' 카테고리의 다른 글
| 12. Lambda Calculus (0) | 2024.06.19 |
|---|---|
| 10. Automatic Type Inference (0) | 2024.06.19 |
| 9. Type System (0) | 2024.06.19 |
| 8. 레코드, 포인터, 메모리 관리(수동, 가비지컬렉션) (0) | 2024.06.19 |
| 7. 명시적 참조 & 암시적 참조 (0) | 2024.06.19 |
