Diffie-Hellman Key Exchange
Diffie-Hellman 키 교환 알고리즘은 안전한 방식으로 공개 네트워크를 통해 비밀 키를 공유할 수 있게 하는 방법이다.
먼저, 큰 소수 q와 mod q에 대한 원시 근 α는 공개적으로 정해져있다.
각 사용자는 먼저 자신의 개인 키 X_a를 선택한다. (1 < X_a < q-1) [여기서 a는 사용자의 이름으로, 반대 편은 X_b이다. 이하 생략]
공개 키 Y_a = α^X_a mod q 이다.
생성된 공개 키 Y_a는 모든 사용자에게 공개된다.
A가 B에게 Y_a를 전달하면, B가 A와 통신하기 위해 사용할 비밀 키 K는, K = Y_a^X_b mod q 가 된다.
이는 α^(X_a * X_b) mod q와 같다.
반대로, B가 Y_b를 전달하면, A가 B와 통신하기 위해 사용할 비밀 키 K는, K = Y_b^X_a mod q 가 된다.
이는 α^(X_a * X_b) mod q와 같다.
즉, 상대방에 공개 키에 자신의 개인 키를 제곱해줌으로써 상대방과의 비밀 키 K를 구할 수 있다.
취약점에 대한 공격으로부터, 통신 시마다 임의의 개인/공개 키를 생성하는 방법이 있다. 이는 키가 노출되더라도 이전이후 통신 내용이 위험에 노출되지 않는다. 다만 이는 매우 느리다.
또, 고정된 개인 키와 공개 키를 생성하고 이를 디렉토리나 데이터베이스같은 공개적으로 접근 가능한 장소에 저장하고 사용할 수도 있다.
그러나 위 두 방법 모두 man-in-the-middle attack(중간자 공격)에 취약하다.
중간자 공격이란, 공격자가 통신하는 양측 사이에 끼어들어 각자와 독립적으로 통신을 진행하며 양측이 서로 통신하고 있다고 착각하게 만드는 공격 방법이다. 이를 해결하기 위해 키의 인증이 필요하다.
ElGamal Cryptography
Elgamal 암호 시스템은 diffie-hellman 키 교환과 관련이 깊은 공개 키 암호화 방식이다.
각 사용자는 자신의 개인 키 X_a 을 선택한다. (1 < X_a < q-1)
그리고 공개 키 Y_a = α^X_a mod q를 구한다.
**암호화**
보낼 메시지 M은 0 <= M <= q-1 범위에 있다. (q-1을 넘어가면 mod q로 인해 데이터 손실)
랜덤 정수 k를 구한다. (1 < k < q-1)
일회용 키 K를 구한다. K = Y_a ^k mod q (Y_a는 수신자의 공개 키이다.)
M을 두 정수의 쌍 (C1, C2)로 암호화한다.
C1 = α^k mod q
C2 = KM mod q
여기서 C1은 공개키 α를 사용하여 계산되며, C2는 일회용 키 K와 메시지 M을 결합하여 생성된다.
**복호화**
수신자는 받은 C1을 사용하여 일회용 키 K를 복구한다. K = C1 ^ X_a mod q이다. (X_a는 수신자의 개인 키이다.)
수신자는 복구된 키 K를 사용하여 원래 메시지 M을 계산한다.
M = C2 * K^-1 mod q
Elliptic Curve Cryptography
타원 곡선 암호화는 공개 키 암호화의 한 형태로, RSA나 Diffie-Hellman과 같은 기존의 공개 키 암호화 방식과 달리 타원 곡선 수학을 기반으로 한다.
255bit의 ECC 키는 3072bit의 RSA와 비슷한 보안 수준을 제공함으로, 키와 메시지의 저장 및 처리에 필요한 컴퓨터 자원을 상당히 줄여준다.
ECC는 특정한 형태의 타원 곡선과 이 곡선 위의 점들 간의 연산을 암호화의 기초로 사용한다. 이러한 연산은 이산 로그 문제의 타원 곡선 버전에 기반을 둔다.
비교적 최신 기술로, 아직 분석과 실적용 사례는 적은 편이다.
실제 타원 곡선은 두 변수 x와 y를 포함하는 방정식으로 정의된다. 일반적인 형태의 3차 타원 곡선은 y^2 = x^3 +ax + b의 형태로 나타나며, x, y, a, b는 모두 실수이다. 여기서 a와 b는 곡선의 형태를 결정하는 상수이다.
타원 곡선 E(a,b)는 이 방정식을 만족하는 모든 점들의 집합이다. 이러한 점들은 암호화 연산에서 사용된다.
타원 곡선 암호화에서는 zero point라 불리는 O를 정의한다. 이는 타원 곡선에서의 덧셈에 대한 항등원이다.
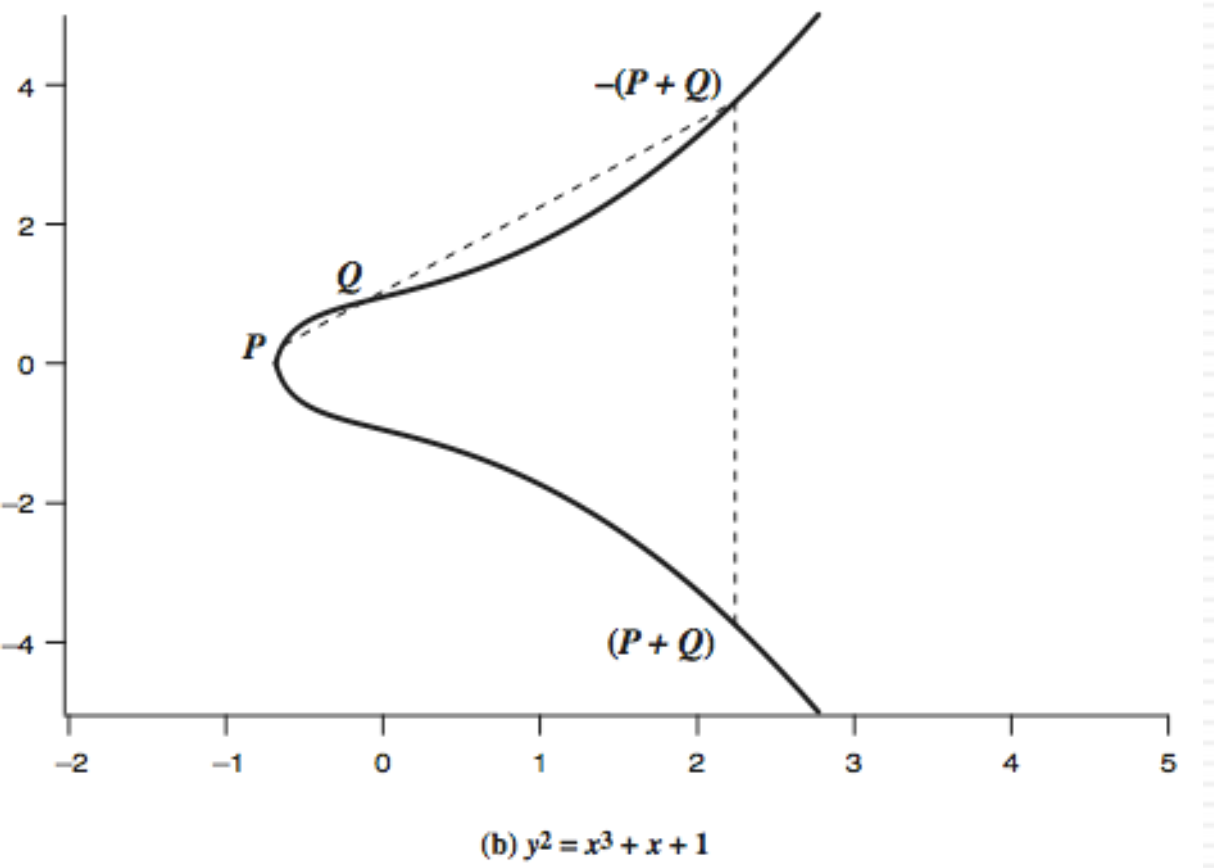
타원 곡선에서 덧셈은 두 점을 지나는 직선을 그리고 그 직선이 타원 곡선과 만나는 세 번째 점 R을 x축에 대해 반사시킨 점이다.
이를 식으로 정리하면,
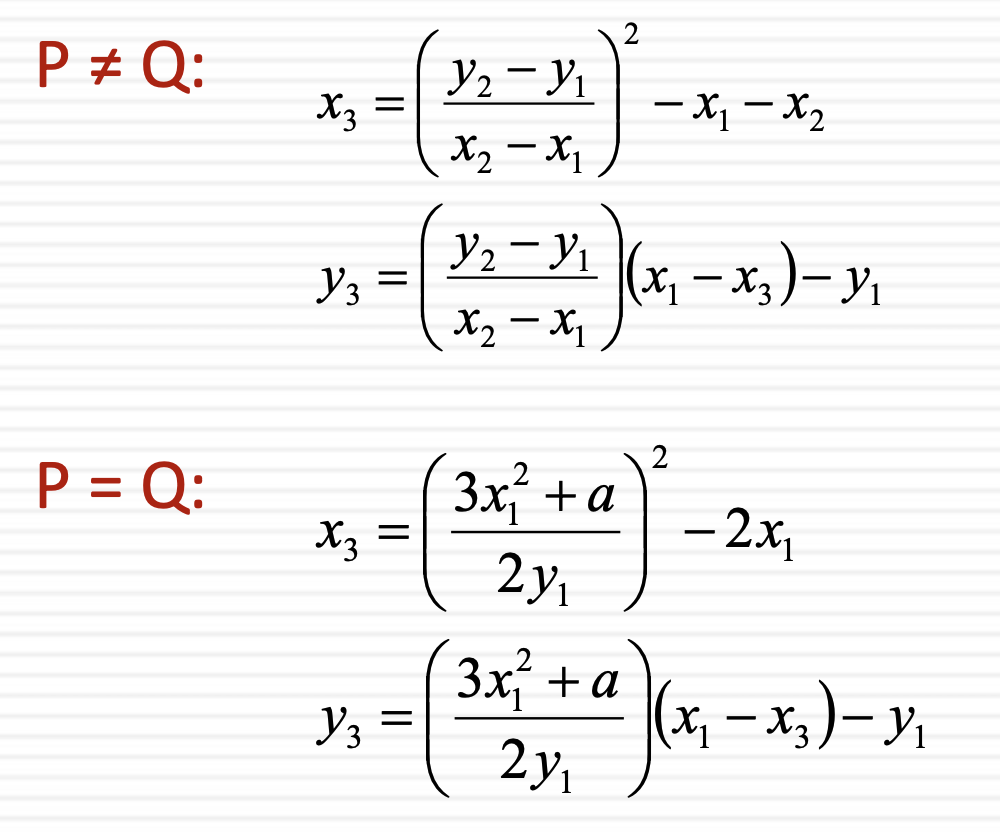
위와 같은 식이 나온다.
유한 타원 곡선 암호화는 변수와 계수가 유한한 집합에 속하는 타원 곡선을 사용한다. 이러한 유한 타원 곡선은 소수 곡선과 이진 곡선으로 분류된다.
소수 곡선은, Zp 상에 정의되며 여기서 p는 소수이다.이 곡선은 Ep(a,b)로 정의되고, 방정식 y^2 = x^3 + ax + b에 대해 x,y,a,b는 모두 Zp의 원소이다. 이는 정수를 소수 p에 대한 모듈러로 사용한다는 뜻이다. 이는 소프트웨어에서 적합하다.
이진 곡선은, GF(2^n)상에 정의되며 E_2^n(a, b)로 표현되고 방정식은 일반적으로 y^2 + xy = x^3 + ax^2 + b 형태를 띈다. 여기서 a, b, x, y는 GF(2^n)의 원소로, 이진 계수를 갖는 다항식으로 표현된다. 이는 하드웨어에서 적합하다.
ECC의 보안성은 타원 곡선 로그 문제에 기반을 둔다.
주어진 한 점 P에 대해, 정수 k를 곱하여 점 Q를 계산하는 것은 비교적 쉬운 연산이다. 이는 Q = kP로 표현된다.
하지만 Q와 P가 주어졌을 때, k를 찾는 것은 매우 어렵다.
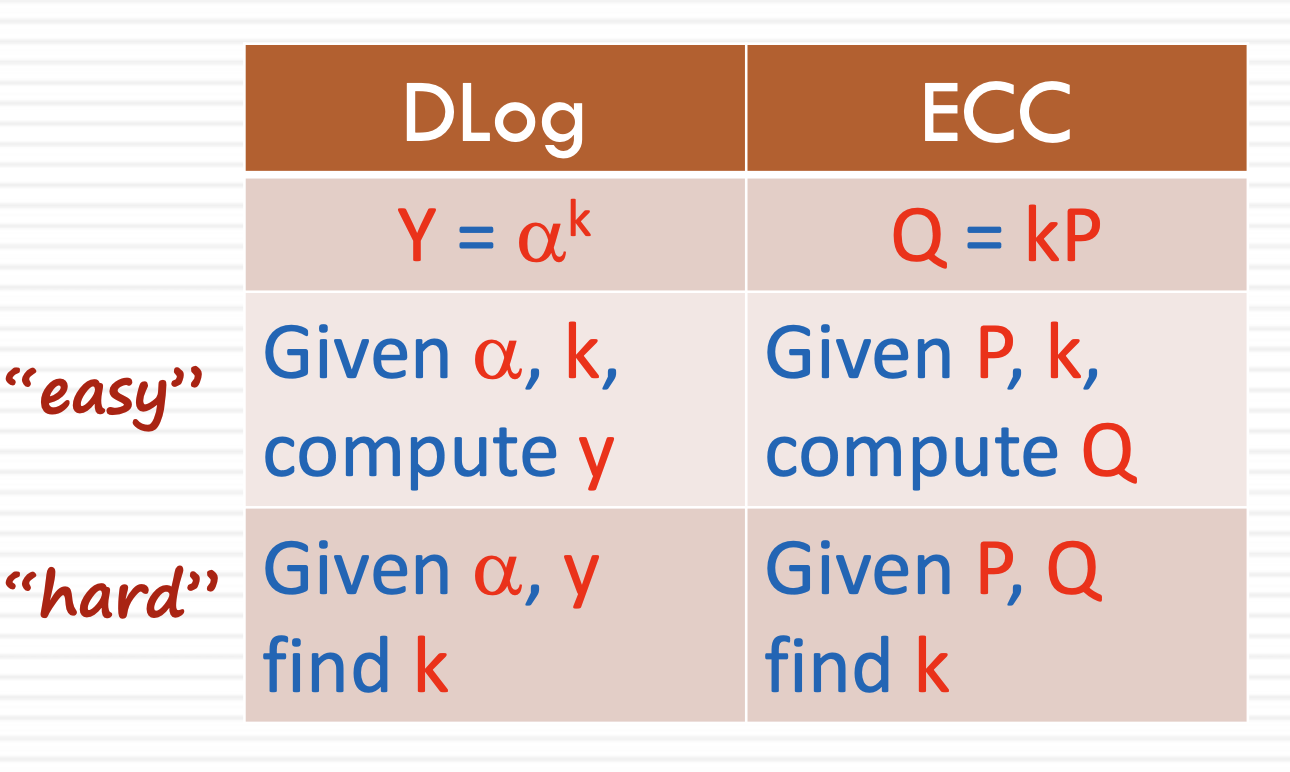
위 그림은 ElGamel 암호화 시스템과 ECC 암호화 시스템에서 쉬운 연산과 어려운 연산을 정리한 것이다.
ECC Diffie-Hellman
Diffie-Hellman 프로토콜을 타원 곡선 상에서 구현한 것이다.
Eq(a,b)형태를 가진 적절한 타원 곡선을 선택한다. 여기서 q는 소수이거나 2의 거듭제곱일 수 있다.
기저점 G=(x,y)를 선택한다. 이 점은 큰 차수 n에 대해 nG = O 를 만족해야한다.
사용자 A와 B는 각각 N_a와 N_b라는 개인 키를 선택한다. 이 값들은 n보다 작은 정수여야한다.
공개 키 P_a = N_a * G, P_b = N_b * G 를 구한다.
이제 공유 키 K = N_a * P_b = N_b * P_a = N_a * N_b * G를 구할 수 있다.
공격자가 공유 키를 계산하려면 주어진 기저점 G와 공개키 P_a 또는 P_b (즉, kG)를 사용하여 개인 키 N_a 또는 N_b (즉, k)를 찾아야 한다. 이는 타원 곡선 로그 문제로 어렵다.
ECC Ecryption/Decryption
ECC로 메시지를 암복호화할 수 있다.
암호화 하려는 메시지 M을 타원 곡선 상의 점 Pm으로 인코딩한다.
적합한 타원 곡선과 기저점 G를 구한다.
각 사용자는 n보다 작은 개인 키 N_a를 선택한다.
공개 키 P_a = N_a * G이다.
암호화는 무작위 k를 선택하고, 두 점의 쌍 Cm = {kG, Pm + kP_a}를 계산한다.
복호화는 자신의 개인 키 N_a를 사용하여 두 번째 점에서 첫 번째 점을 뺀다. Pm + kP_a - N_a(kG)
이를 단순화하면 Pm + k(N_a * G) - N_a(kG)가 된다.
'학교강의필기장 > 암호학' 카테고리의 다른 글
| 11. Message Authentication (2) | 2023.12.07 |
|---|---|
| 10. Hash Functions (2) | 2023.12.06 |
| 8. 모듈러/정수론 정리 (1) | 2023.10.20 |
| 7. public key system (0) | 2023.10.18 |
| 6. number theory (1) | 2023.10.17 |
Diffie-Hellman Key Exchange
Diffie-Hellman 키 교환 알고리즘은 안전한 방식으로 공개 네트워크를 통해 비밀 키를 공유할 수 있게 하는 방법이다.
먼저, 큰 소수 q와 mod q에 대한 원시 근 α는 공개적으로 정해져있다.
각 사용자는 먼저 자신의 개인 키 X_a를 선택한다. (1 < X_a < q-1) [여기서 a는 사용자의 이름으로, 반대 편은 X_b이다. 이하 생략]
공개 키 Y_a = α^X_a mod q 이다.
생성된 공개 키 Y_a는 모든 사용자에게 공개된다.
A가 B에게 Y_a를 전달하면, B가 A와 통신하기 위해 사용할 비밀 키 K는, K = Y_a^X_b mod q 가 된다.
이는 α^(X_a * X_b) mod q와 같다.
반대로, B가 Y_b를 전달하면, A가 B와 통신하기 위해 사용할 비밀 키 K는, K = Y_b^X_a mod q 가 된다.
이는 α^(X_a * X_b) mod q와 같다.
즉, 상대방에 공개 키에 자신의 개인 키를 제곱해줌으로써 상대방과의 비밀 키 K를 구할 수 있다.
취약점에 대한 공격으로부터, 통신 시마다 임의의 개인/공개 키를 생성하는 방법이 있다. 이는 키가 노출되더라도 이전이후 통신 내용이 위험에 노출되지 않는다. 다만 이는 매우 느리다.
또, 고정된 개인 키와 공개 키를 생성하고 이를 디렉토리나 데이터베이스같은 공개적으로 접근 가능한 장소에 저장하고 사용할 수도 있다.
그러나 위 두 방법 모두 man-in-the-middle attack(중간자 공격)에 취약하다.
중간자 공격이란, 공격자가 통신하는 양측 사이에 끼어들어 각자와 독립적으로 통신을 진행하며 양측이 서로 통신하고 있다고 착각하게 만드는 공격 방법이다. 이를 해결하기 위해 키의 인증이 필요하다.
ElGamal Cryptography
Elgamal 암호 시스템은 diffie-hellman 키 교환과 관련이 깊은 공개 키 암호화 방식이다.
각 사용자는 자신의 개인 키 X_a 을 선택한다. (1 < X_a < q-1)
그리고 공개 키 Y_a = α^X_a mod q를 구한다.
**암호화**
보낼 메시지 M은 0 <= M <= q-1 범위에 있다. (q-1을 넘어가면 mod q로 인해 데이터 손실)
랜덤 정수 k를 구한다. (1 < k < q-1)
일회용 키 K를 구한다. K = Y_a ^k mod q (Y_a는 수신자의 공개 키이다.)
M을 두 정수의 쌍 (C1, C2)로 암호화한다.
C1 = α^k mod q
C2 = KM mod q
여기서 C1은 공개키 α를 사용하여 계산되며, C2는 일회용 키 K와 메시지 M을 결합하여 생성된다.
**복호화**
수신자는 받은 C1을 사용하여 일회용 키 K를 복구한다. K = C1 ^ X_a mod q이다. (X_a는 수신자의 개인 키이다.)
수신자는 복구된 키 K를 사용하여 원래 메시지 M을 계산한다.
M = C2 * K^-1 mod q
Elliptic Curve Cryptography
타원 곡선 암호화는 공개 키 암호화의 한 형태로, RSA나 Diffie-Hellman과 같은 기존의 공개 키 암호화 방식과 달리 타원 곡선 수학을 기반으로 한다.
255bit의 ECC 키는 3072bit의 RSA와 비슷한 보안 수준을 제공함으로, 키와 메시지의 저장 및 처리에 필요한 컴퓨터 자원을 상당히 줄여준다.
ECC는 특정한 형태의 타원 곡선과 이 곡선 위의 점들 간의 연산을 암호화의 기초로 사용한다. 이러한 연산은 이산 로그 문제의 타원 곡선 버전에 기반을 둔다.
비교적 최신 기술로, 아직 분석과 실적용 사례는 적은 편이다.
실제 타원 곡선은 두 변수 x와 y를 포함하는 방정식으로 정의된다. 일반적인 형태의 3차 타원 곡선은 y^2 = x^3 +ax + b의 형태로 나타나며, x, y, a, b는 모두 실수이다. 여기서 a와 b는 곡선의 형태를 결정하는 상수이다.
타원 곡선 E(a,b)는 이 방정식을 만족하는 모든 점들의 집합이다. 이러한 점들은 암호화 연산에서 사용된다.
타원 곡선 암호화에서는 zero point라 불리는 O를 정의한다. 이는 타원 곡선에서의 덧셈에 대한 항등원이다.

타원 곡선에서 덧셈은 두 점을 지나는 직선을 그리고 그 직선이 타원 곡선과 만나는 세 번째 점 R을 x축에 대해 반사시킨 점이다.
이를 식으로 정리하면,
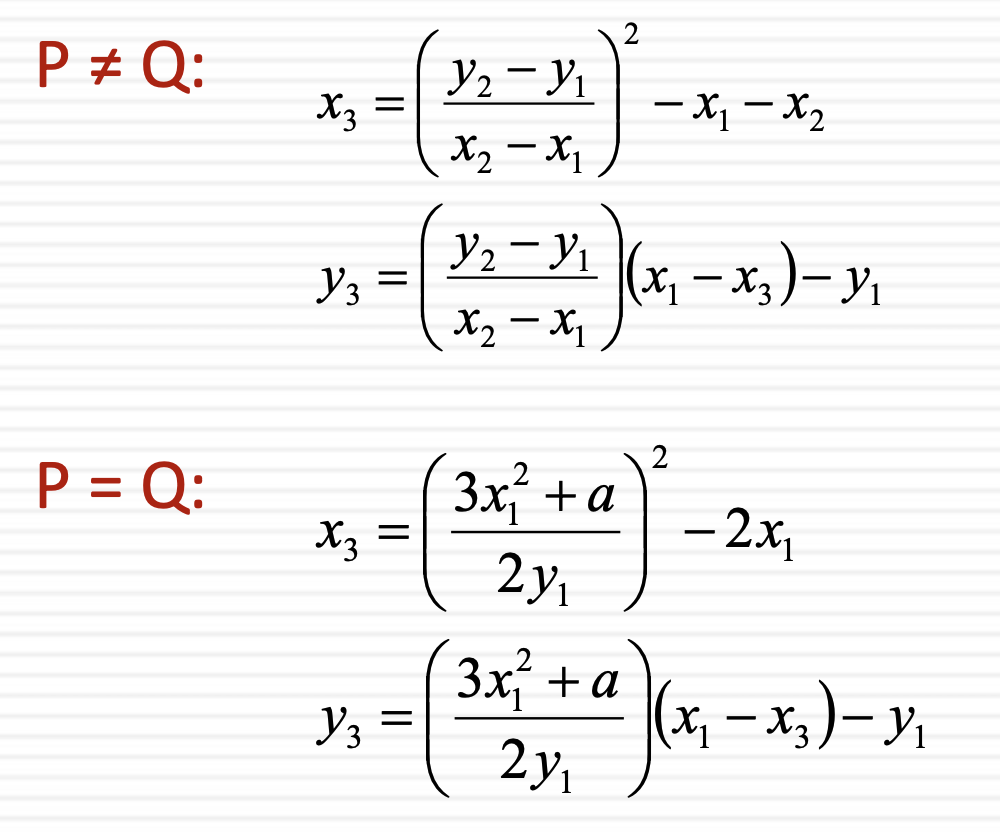
위와 같은 식이 나온다.
유한 타원 곡선 암호화는 변수와 계수가 유한한 집합에 속하는 타원 곡선을 사용한다. 이러한 유한 타원 곡선은 소수 곡선과 이진 곡선으로 분류된다.
소수 곡선은, Zp 상에 정의되며 여기서 p는 소수이다.이 곡선은 Ep(a,b)로 정의되고, 방정식 y^2 = x^3 + ax + b에 대해 x,y,a,b는 모두 Zp의 원소이다. 이는 정수를 소수 p에 대한 모듈러로 사용한다는 뜻이다. 이는 소프트웨어에서 적합하다.
이진 곡선은, GF(2^n)상에 정의되며 E_2^n(a, b)로 표현되고 방정식은 일반적으로 y^2 + xy = x^3 + ax^2 + b 형태를 띈다. 여기서 a, b, x, y는 GF(2^n)의 원소로, 이진 계수를 갖는 다항식으로 표현된다. 이는 하드웨어에서 적합하다.
ECC의 보안성은 타원 곡선 로그 문제에 기반을 둔다.
주어진 한 점 P에 대해, 정수 k를 곱하여 점 Q를 계산하는 것은 비교적 쉬운 연산이다. 이는 Q = kP로 표현된다.
하지만 Q와 P가 주어졌을 때, k를 찾는 것은 매우 어렵다.

위 그림은 ElGamel 암호화 시스템과 ECC 암호화 시스템에서 쉬운 연산과 어려운 연산을 정리한 것이다.
ECC Diffie-Hellman
Diffie-Hellman 프로토콜을 타원 곡선 상에서 구현한 것이다.
Eq(a,b)형태를 가진 적절한 타원 곡선을 선택한다. 여기서 q는 소수이거나 2의 거듭제곱일 수 있다.
기저점 G=(x,y)를 선택한다. 이 점은 큰 차수 n에 대해 nG = O 를 만족해야한다.
사용자 A와 B는 각각 N_a와 N_b라는 개인 키를 선택한다. 이 값들은 n보다 작은 정수여야한다.
공개 키 P_a = N_a * G, P_b = N_b * G 를 구한다.
이제 공유 키 K = N_a * P_b = N_b * P_a = N_a * N_b * G를 구할 수 있다.
공격자가 공유 키를 계산하려면 주어진 기저점 G와 공개키 P_a 또는 P_b (즉, kG)를 사용하여 개인 키 N_a 또는 N_b (즉, k)를 찾아야 한다. 이는 타원 곡선 로그 문제로 어렵다.
ECC Ecryption/Decryption
ECC로 메시지를 암복호화할 수 있다.
암호화 하려는 메시지 M을 타원 곡선 상의 점 Pm으로 인코딩한다.
적합한 타원 곡선과 기저점 G를 구한다.
각 사용자는 n보다 작은 개인 키 N_a를 선택한다.
공개 키 P_a = N_a * G이다.
암호화는 무작위 k를 선택하고, 두 점의 쌍 Cm = {kG, Pm + kP_a}를 계산한다.
복호화는 자신의 개인 키 N_a를 사용하여 두 번째 점에서 첫 번째 점을 뺀다. Pm + kP_a - N_a(kG)
이를 단순화하면 Pm + k(N_a * G) - N_a(kG)가 된다.
'학교강의필기장 > 암호학' 카테고리의 다른 글
| 11. Message Authentication (2) | 2023.12.07 |
|---|---|
| 10. Hash Functions (2) | 2023.12.06 |
| 8. 모듈러/정수론 정리 (1) | 2023.10.20 |
| 7. public key system (0) | 2023.10.18 |
| 6. number theory (1) | 2023.10.17 |
