https://www.acmicpc.net/problem/17268
17268번: 미팅의 저주
인하대 컴퓨터 공학과에 재학 중인 이산이는 오랜만에 미팅을 나가 볼까 한다. 미팅은 N명이 원탁에 앉아서 진행된다고 한다. 질투가 난 이산이 친구 명기는 X의 저주를 걸었다. 그 저주는 N명이 동시에 2명씩 짝을 지어 악수할 때 사람의 팔이 교차되거나 한 사람이라도 악수를 하지 못하면 그 미팅은 실패하게 되는 저주다. 하지만 명기는 이산이에게 저주를 풀 기회를 주었다. 미팅에 성공할 경우의 수를 구하여 큰소리로 외치면 저주가 풀린다. 하지만 이산이는 계산
www.acmicpc.net

짝수의 사람이 둘 씩 짝지어 악수를 할 때, 둘을 이은 선들이 겹치지 않는 경우의 수를 구하는 문제이다.
머리속으로 바로 상상하기는 힘드므로, 입력 최소값인 2부터 그려보자.
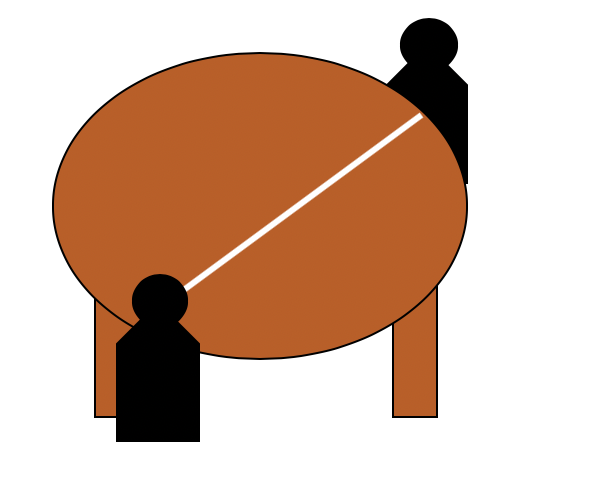
2명일때의 경우의 수는 1이다.
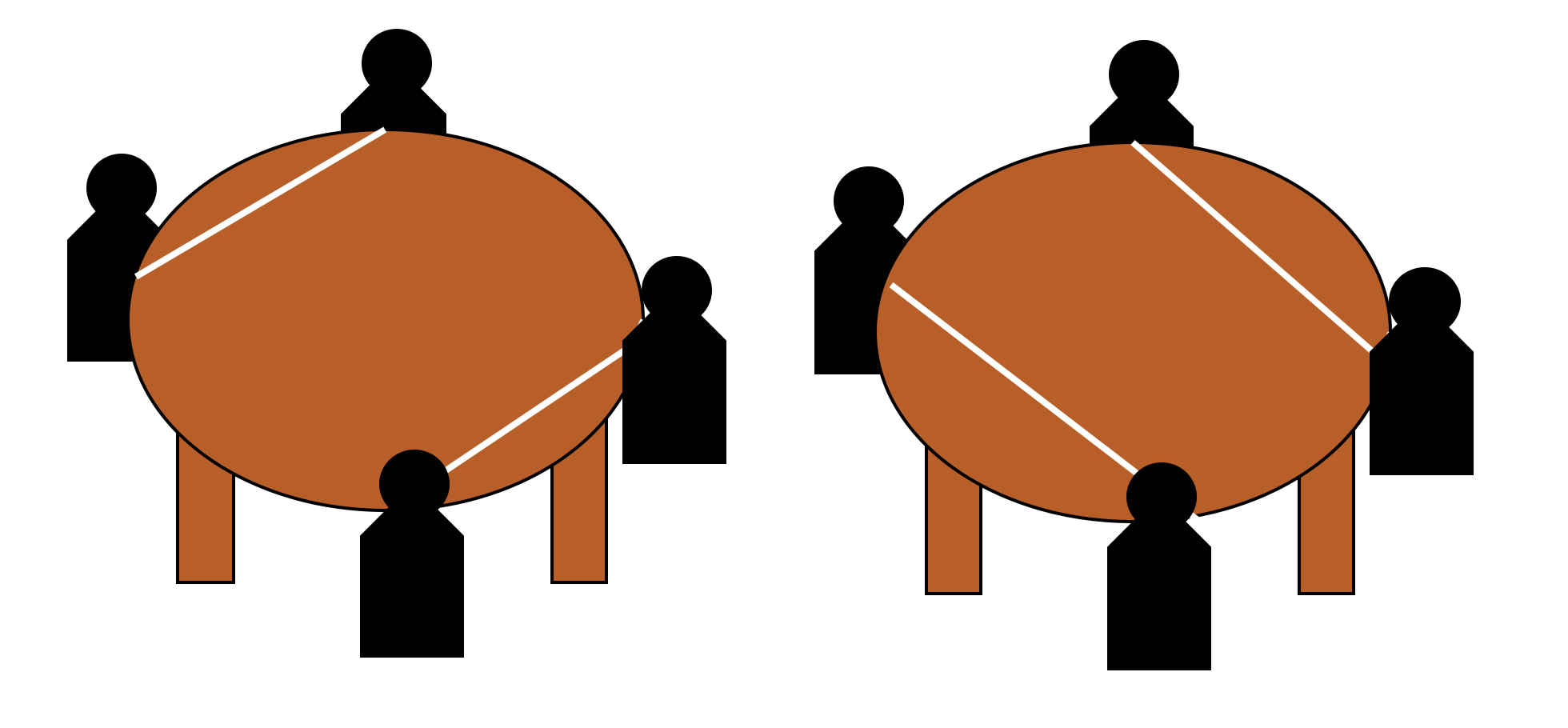
4명일때의 경우의 수는 2이다.
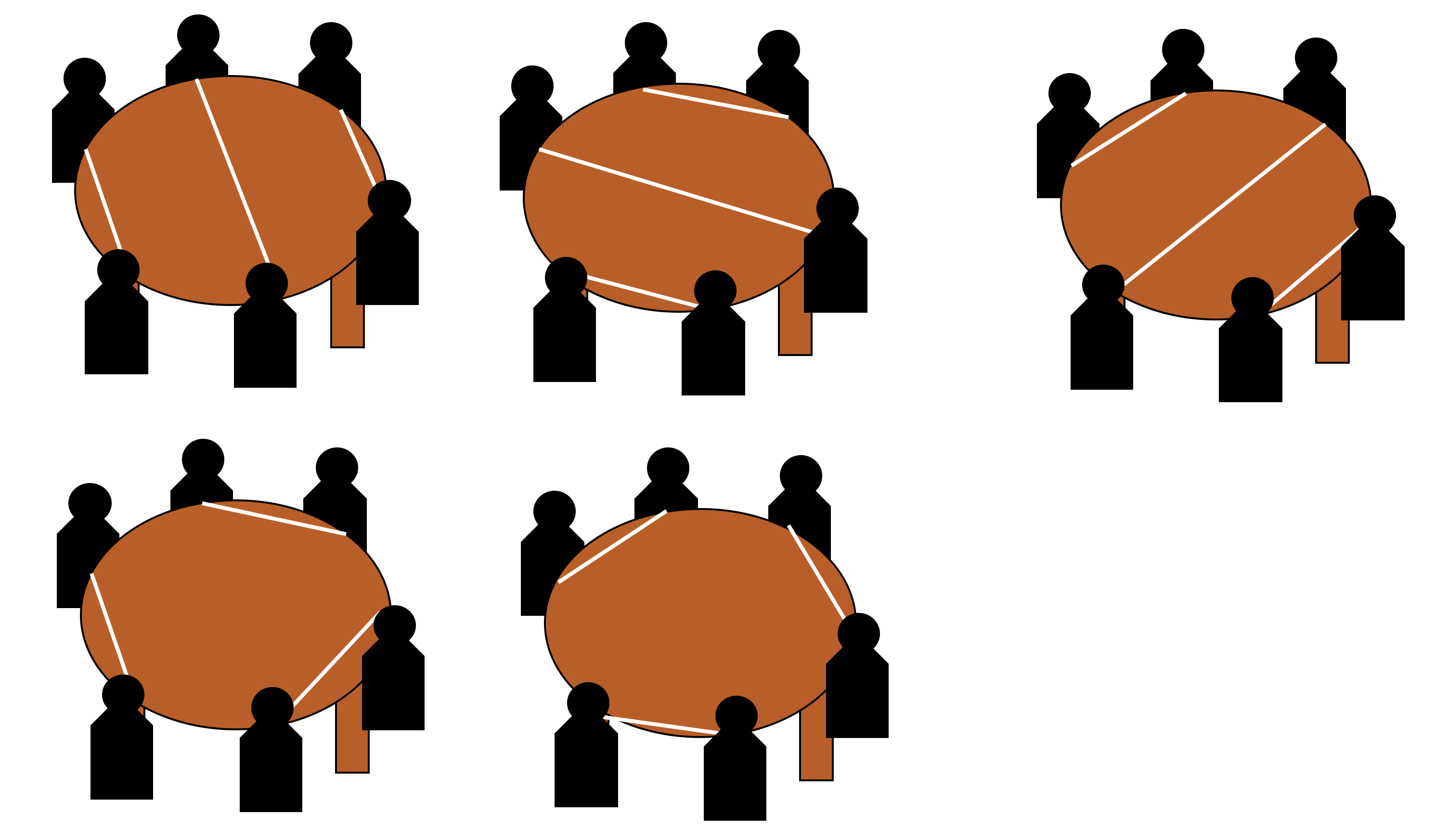
6명일 때의 경우의 수는 5이다



8명이서 악수하는 경우의 수는 14이다.
정리하자면,
2명일 때 1, 4명일 때 2, 6명일 때 5, 8명일 때 14이다.
즉 (1, 2, 5, 14, ...)
이에 해당하는 수열은, 카탈란 수이다.
카탈란 수의 점화식은 C(0)=1, C(n) = Sigma(n-1, i=0) {C(i)*C(n-i-1)} 이다.
단, 입력 받는 수는 n의 2배임을 주의한다.
수가 매우 커지기도 하고, 문제에서도 나머지를 취하라고 하니 매 연산마다 나머지를 취해줌으로 오버플로우를 방지해준다.
또한, 곱셈 과정에서 int범위를 초과할 수 있으므로 long long으로 받아주도록 한다.
카탈란 수에 대한 자세한 설명은 위키피디아를 참고하면 되겠다.
https://ko.wikipedia.org/wiki/%EC%B9%B4%ED%83%88%EB%9E%91_%EC%88%98
#include<iostream>
#include<vector>
#define mod 987654321
using namespace std;
typedef long long ll;
int main(){
int n; cin>>n; n=n/2;
vector <ll> memo(n+1);
memo[0]=1;
for(int i=1; i<=n; i++){
memo[i]=0;
for(int k=0; k<i; k++){
memo[i]+=((memo[k]%mod)*(memo[i-1-k]%mod))%mod;
}
memo[i] %= mod;
}
cout<<memo[n]%mod;
}
'현생 > 백준 온라인 저지' 카테고리의 다른 글
| [백준 2011][DP][C++] 암호코드 (0) | 2019.11.01 |
|---|---|
| [백준 14940][BFS][C++] 쉬운 최단거리 (0) | 2019.10.29 |
| [백준 17267][BFS][C++] 상남자 (0) | 2019.10.27 |
| [백준 1107][브루트포스][C++] 리모컨 (0) | 2019.10.27 |
| [백준 17219][이분탐색][C++] 비밀번호 찾기 (0) | 2019.10.27 |
https://www.acmicpc.net/problem/17268
17268번: 미팅의 저주
인하대 컴퓨터 공학과에 재학 중인 이산이는 오랜만에 미팅을 나가 볼까 한다. 미팅은 N명이 원탁에 앉아서 진행된다고 한다. 질투가 난 이산이 친구 명기는 X의 저주를 걸었다. 그 저주는 N명이 동시에 2명씩 짝을 지어 악수할 때 사람의 팔이 교차되거나 한 사람이라도 악수를 하지 못하면 그 미팅은 실패하게 되는 저주다. 하지만 명기는 이산이에게 저주를 풀 기회를 주었다. 미팅에 성공할 경우의 수를 구하여 큰소리로 외치면 저주가 풀린다. 하지만 이산이는 계산
www.acmicpc.net

짝수의 사람이 둘 씩 짝지어 악수를 할 때, 둘을 이은 선들이 겹치지 않는 경우의 수를 구하는 문제이다.
머리속으로 바로 상상하기는 힘드므로, 입력 최소값인 2부터 그려보자.

2명일때의 경우의 수는 1이다.

4명일때의 경우의 수는 2이다.

6명일 때의 경우의 수는 5이다



8명이서 악수하는 경우의 수는 14이다.
정리하자면,
2명일 때 1, 4명일 때 2, 6명일 때 5, 8명일 때 14이다.
즉 (1, 2, 5, 14, ...)
이에 해당하는 수열은, 카탈란 수이다.
카탈란 수의 점화식은 C(0)=1, C(n) = Sigma(n-1, i=0) {C(i)*C(n-i-1)} 이다.
단, 입력 받는 수는 n의 2배임을 주의한다.
수가 매우 커지기도 하고, 문제에서도 나머지를 취하라고 하니 매 연산마다 나머지를 취해줌으로 오버플로우를 방지해준다.
또한, 곱셈 과정에서 int범위를 초과할 수 있으므로 long long으로 받아주도록 한다.
카탈란 수에 대한 자세한 설명은 위키피디아를 참고하면 되겠다.
https://ko.wikipedia.org/wiki/%EC%B9%B4%ED%83%88%EB%9E%91_%EC%88%98
#include<iostream>
#include<vector>
#define mod 987654321
using namespace std;
typedef long long ll;
int main(){
int n; cin>>n; n=n/2;
vector <ll> memo(n+1);
memo[0]=1;
for(int i=1; i<=n; i++){
memo[i]=0;
for(int k=0; k<i; k++){
memo[i]+=((memo[k]%mod)*(memo[i-1-k]%mod))%mod;
}
memo[i] %= mod;
}
cout<<memo[n]%mod;
}
'현생 > 백준 온라인 저지' 카테고리의 다른 글
| [백준 2011][DP][C++] 암호코드 (0) | 2019.11.01 |
|---|---|
| [백준 14940][BFS][C++] 쉬운 최단거리 (0) | 2019.10.29 |
| [백준 17267][BFS][C++] 상남자 (0) | 2019.10.27 |
| [백준 1107][브루트포스][C++] 리모컨 (0) | 2019.10.27 |
| [백준 17219][이분탐색][C++] 비밀번호 찾기 (0) | 2019.10.27 |
