Digital Signatures
디지털 서명은 서명자, 서명 날짜 및 시간을 확인할 수 있고 메시지 내용의 인증이 가능하며, 제삼자가 검증할 수 있다.
정리하자면, 추가 기능을 갖춘 인증 기능을 포함한다.
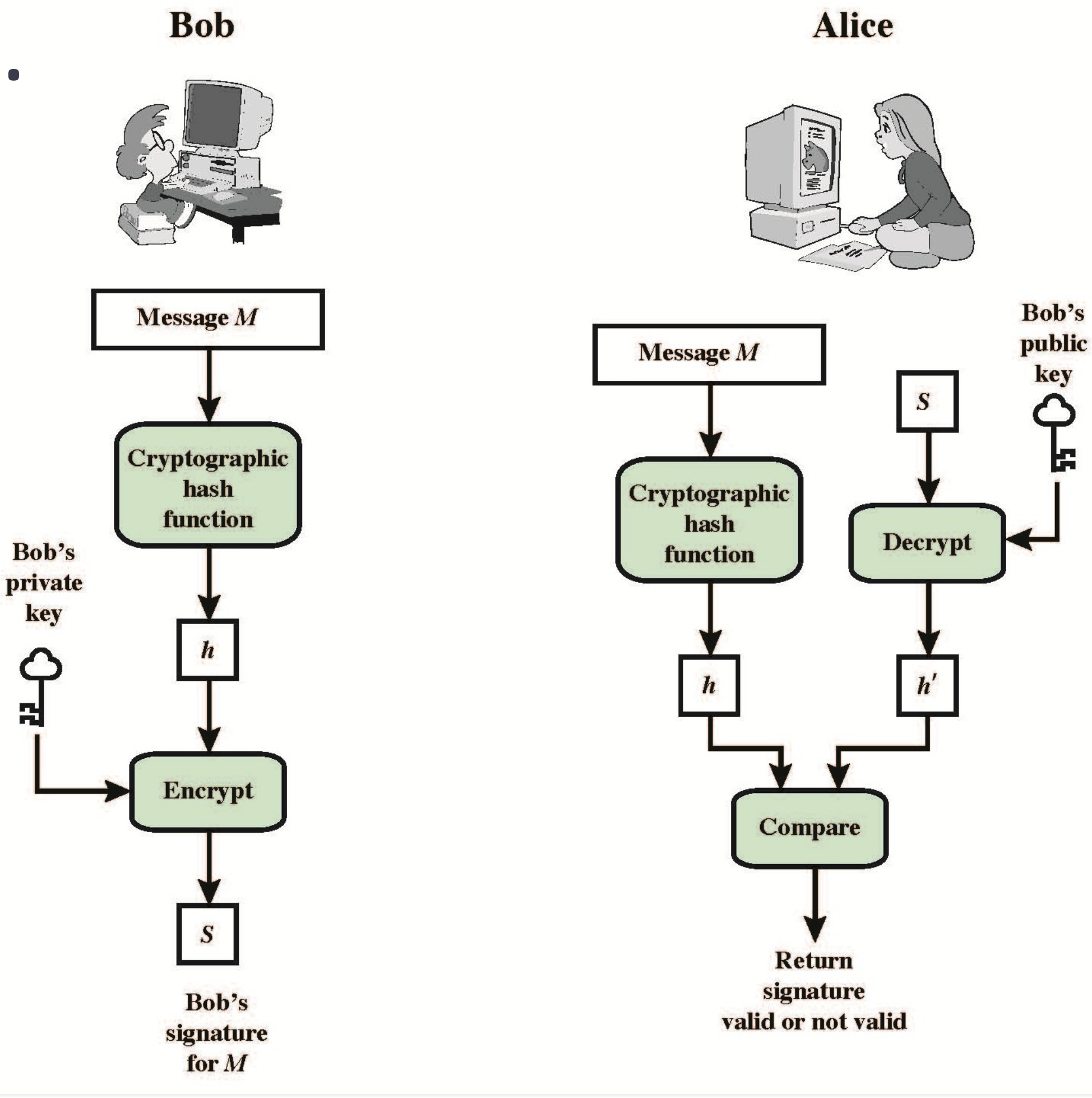
이러한 디지털 서명 방법으로 메시지를 해시한 값을 발신자의 개인키로 암호화한 S를 보내고,
수신자는 받은 메시지를 해시한 값과 S를 발신자의 공개키로 복호화한 값을 비교하여 검증하는 방법을 떠올릴 수 있다.
디지털 서명은 여러 방법으로 공격당할 수 있다.
1. Key only attack: 공격자가 대상의 공개키만을 알고 있을 때
2. Known message attack: 공격자가 일련의 메시지와 그에 대한 서명들을 알고 있을 때
3. Chosen message attack: 공격자가 선택한 메시지에 대한 유효한 서명을 얻을 수 있을 때
4. Adaptive chosen message attack: 공격자는 이전에 얻은 메시지-서명 쌍에 따라 달라지는 메시지에 대한 유효한 서명을 얻을 수 있을 때
또, 다양한 종류의 디지털 서명 위조 방법이 있다.
1. Total break(전체 파괴): 공격자가 대상의 개인 키를 알아내는 경우
2. Universal forgery(전체 위조): 공격자가 서명을 생성하는 효율적인 알고리즘을 찾아내서 서명을 구성하는 동등한 방법 제공
3. Selective forgery(선택적 위조): 공격자가 특정 메시지에 대한 서명을 위조
4. Existential forgery(존재적 위조): 공격자가 적어도 하나의 메시지에 대한 서명을 위조하지만, 메시지의 내용에 대한 제어는 불가
Digital Signature Requirements
1. 서명은 메시지에 의존해서 생성되어야 한다.
2. 발신자에게 고유한 정보를 사용해야 한다 => 위조와 부인 방지를 위해 발신자만이 가지고 있는 정보를 사용해야 함
3. 생성이 상대적으로 쉬워야 한다.
4. 인식 및 검증이 상대적으로 쉬워야 한다.
5. 새 메시지에 대해 기존 디지털 서명을 사용한 위조가 불가능해야 한다.
6. 저장 공간에 디지털 서명을 실용적으로 보관할 수 있어야 한다.
Elgamal Digital Signature
엘가말 디지털 서명은 엘가말 알고리즘의 서명 변형으로, 디피헬만과 관련이 있으며 갈루아필드에서 지수승을 사용한다.
이 알고리즘의 보안은 디피헬만과 마찬가지로 이산 로그 문제에 기반한다.
개인키를 사용하여 암호화하고, 공개키를 사용하여 복호화한다.
각 사용자는 자신의 키를 생성하며, 개인 키를 1 < Xa < q-1에서 랜덤으로 선택한다.
공개 키를 계산한다. Ya = α^Xa mod q
Alice가 메시지 M을 서명할 때, 먼저 메시지 M을 해시하여 H(M)을 만든다. 여기서 0 <= H(M) <= q-1 이여야 한다.
랜덤 정수 K를 선택한다. 이 때, K는 1 <= K <= (q-1) && gcd(K, q-1) = 1 을 만족해야 한다. 즉, K와 q-1은 서로소여야 한다.
임시 키 S1을 계산한다. S1 = α^K mod q
mod (q-1)에서의 K의 역원 K^-1 mod (q-1)을 계산한다.
S2값을 계산한다. S2 = K^-1 * (H(M) - Xa * S1) mod (q-1) 이다.
여기서 (S1, S2)가 서명이다.
이제 Bob이 서명을 검증한다고 하자.
V1 = α^H(M) mod q
V2 = Ya^S1 * S1^S2 mod q
만약 V1 == V2라면 서명이 유효하다.
Schnorr Digital Signatures
슈노르 디지털 서명은 먼저 적절한 소수 p와 q를 선택한다.
α를 선택하는데, 이 때 α^q ≡ 1 mod p 가 되도록 한다.
개별 사용자의 키 생성은,
개인키 s는 0 < s < q 에서 선택하고, 공개키는 v = α^(-s) mod p 이다.
즉, 공개키 v는 mod p에서 a^s의 역원이다.
임의의 r을 선택한다. ( 0 < r < q )
x = α^r mod p를 계산한다.
메시지 M과 x를 연결한 후 해시 결과를 계산하여 e = H(M || x)를 얻는다.
y = (r + se) mod q를 계산한다. 여기서 서명은 쌍 (e, y) 이다.
검증은 다음과 같이 진행한다.
x' = α^y * v^e mod p
여기서 e와 H(M || x')가 같다면 서명이 유효하다.
Digital Signature Standard (DSS)
DSS는 SHA 해시 알고리즘을 사용하는 디지털 서명 표준이다. DSA 알고리즘이 사용된다.
DSA는 320비트 이상의 서명을 생성하고, 1024비트~3072비트까지의 보안을 제공한다.
RSA보다 작고 빠르며 암호화에는 사용되지 않고 이산 로그 문제의 계산 난이도에 의존한다.
키 생성 과정은 다음과 같다.
공유되는 전역 공개 키값 p, q, g을 구한다.
큰 소수 p를 선택한다. ( 2^(L-1) < p < 2^L )
p-1의 N 비트 소수인 q를 선택한다. ( 2^(N-1) < q < 2^N )
g = h^((p-1)/q) mod p 를 계산한다. (1 < h < p-1, h^((p-1)/q) mod p > 1)
여기서 h는 조건을 만족하는 랜덤값, g는 그룹의 생성자(generator)이다. g는 그룹의 모든 원소를 생성할 수 있다.
사용자의 개인 및 공개 키 생성은 다음과 같다.
개인 키 x 선택 (x<q)
공개 키 y 계산 y = g^x mod p
DSA 서명 생성 과정은 다음과 같다.
1. 임의의 서명키 k 생성 (k < q)
2. 서명 쌍 계산
2-1. r = (g^k mod p) mod q
2-2. s = [k^-1 * (H(M) + xr)] mod q
3. 발신자는 계산된 서명 쌍 (r,s)를 메시지 M과 함께 전송한다.
DSA 서명 검증 과정은 다음과 같다.
1. w = s^-1 mod q
2. u1 = [H(M)w] mod q
3. u2 = (rw) mod q
4. v = [(g^u1 * y^u2) mod p] mod q
만약 v와 r이 같다면 서명이 유효하다.
ECDSA
ECDSA는 타원 곡선 디지털 서명 알고리즘이다.
Key Generation
-. 소수 p를 기반으로 하는 타원 곡선 Ep(a,b)를 선택한다.
-. 기저점 G와 n을 선택한다. 여기서 n은 소수이고, nG는 무한대이다.
임의의 개인 키 d를 선택한다. 0 < d < n
공개 키 Q를 계산한다. Q = dG
ECDSA Signature Creation
1. e = H(M) 단, bitlen(e) <= bitlen(n), bitlen(e)가 더 길다면 잘라낸다.
2. 0 < k < n 에서 k 선택
3. (x1, y1) = kG 계산
4. r = x1 mod n, s = k^-1 * (e + rd) mod n 계산, 만약 r==0 or s==0 이라면 goto 2
5. 서명 쌍 (r, s) 메시지 M과 함께 전송
ECDSA Signature Verification
1. 0<r<n && 0<s<n을 만족하지 않으면 서명 쌍 오류
2. e = H(M)
3. u1 = s^-1 * e mod n
4. u2 = s^-1 * r mod n
5. (x1, y1) = u1G + u2Q
6. (x1, y1)이 무한으로 가면 서명 쌍 오류
7. r≡x1 mod n 이면 서명 유효
RSS-PSS
RSS-PSS는 확률적 서명체계로, 기존의 RSA 서명보다 안전한 것으로 간주된다.
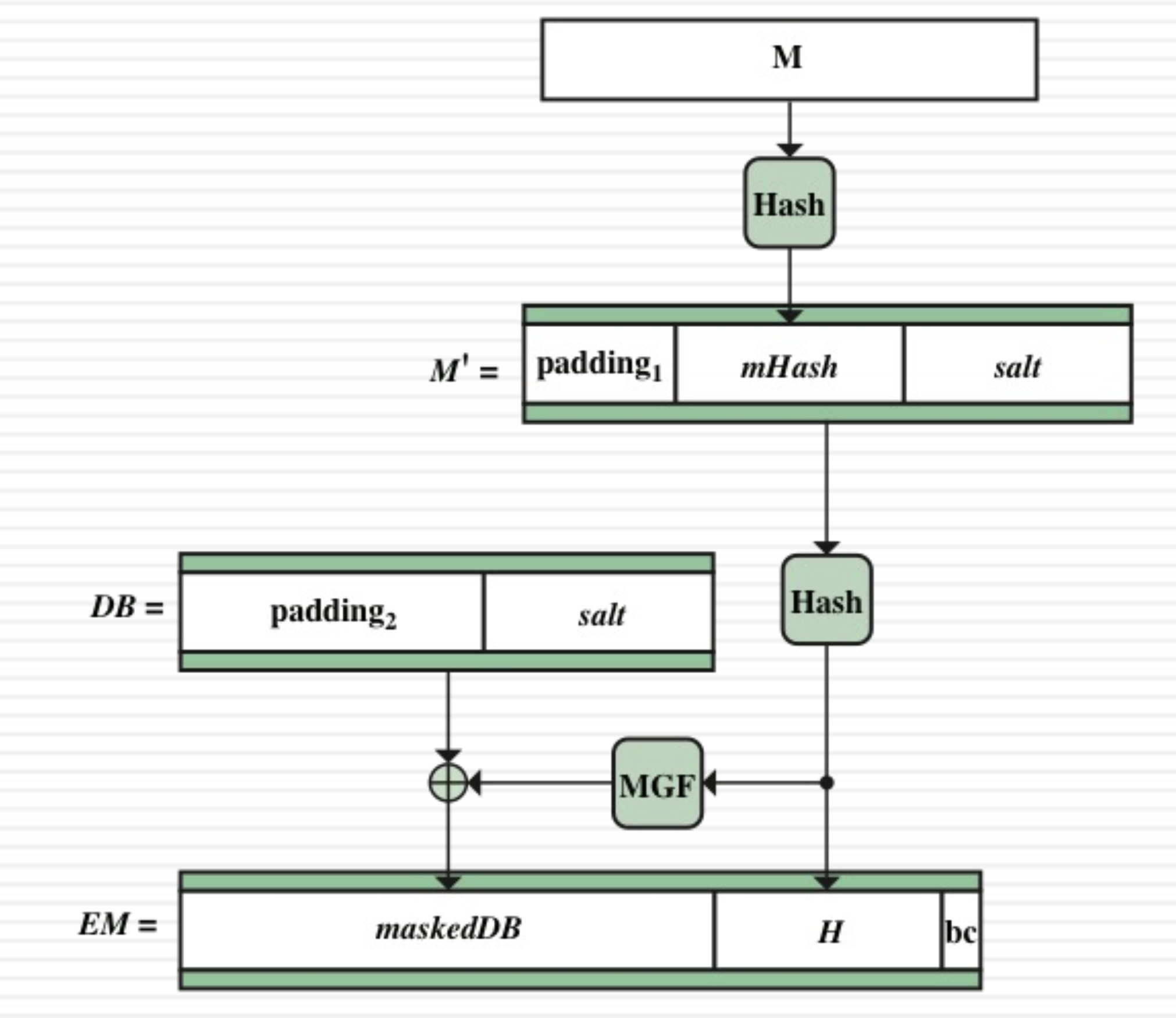
위 그림은 인코딩 방법이다. 먼저 M을 해시하고, M' = [padding || H(M) || salt]를 만든다. 여기서 salt는 랜덤값, padding은 비트의 길이를 일정하게 맞추도록 0으로 채운다.
또 다른 데이터 DB는 비트의 길이가 같고, 앞엔 패딩 뒤엔 이전과 같은 salt가 채워져 있다.
maskedDB = MGF(H(M')) XOR DB이고,
EM = [maskedDB || H(M') || 0xbc ] 이다.
여기서 MGF는 해시함수를 반복적으로 사용하여 원하는 길이의 마스크를 만든다. 시드의 뒤에 0으로부터 시작하는 1워드 크기의 옥텟문자열을 붙이고, 해시할 때마다 이 옥텟문자열을 1씩 늘리며 이어붙여나가기를 원하는 길이가 나올때까지 반복한다.
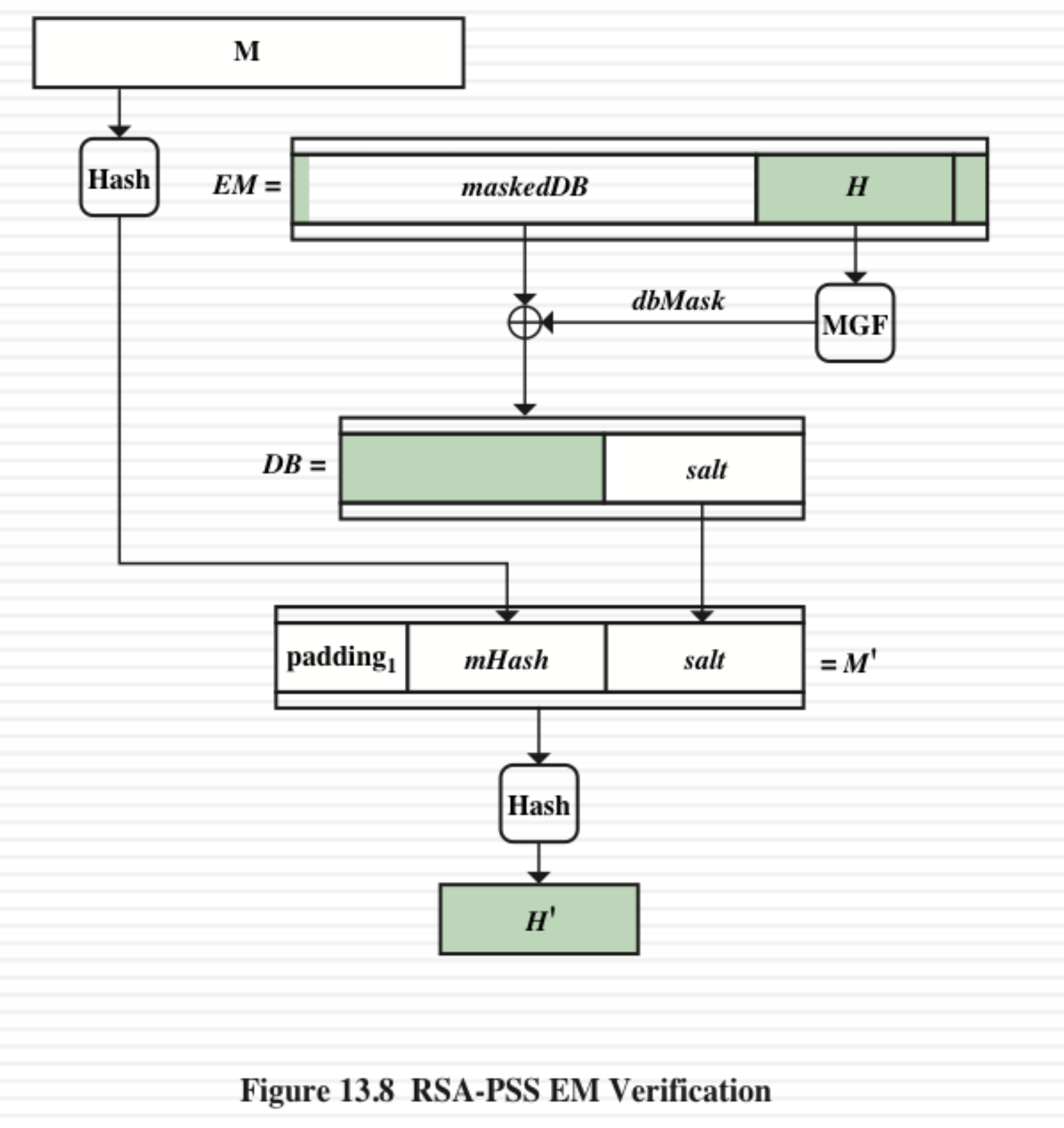
위 그림은 검증 방법이다.
EM에서 maskedDB와 MGF(H(M'))을 XOR하여 DB를 구하고 salt를 구한다.
받은 메시지를 해시하고, M'를 만들고, 구한 salt로 뒤를 채운다.
그걸 해시한 값이 H(M')이 나온다면 검증이 완료된다.
'학교강의필기장 > 암호학' 카테고리의 다른 글
| 14. User Authentication (0) | 2023.12.08 |
|---|---|
| 13. Key Management and Distribution (0) | 2023.12.08 |
| 11. Message Authentication (2) | 2023.12.07 |
| 10. Hash Functions (2) | 2023.12.06 |
| 9. 키 교환 알고리즘과 암복호화 알고리즘, 그리고 타원곡선 (1) | 2023.12.06 |
