귀납적 정의?
귀납적 정의는 프로그래밍 언어의 문법과 의미론, 데이터 구조 등을 이해하고 정의하는데 사용된다. 귀납적 정의는 자기 참조적 정의, 유한한 방법으로 무한 집합 정의의 특징을 가진다.
자기 참조적 정의란 집합이나 구조를 그 자체의 용어로 정의한다. 정의할 대상이 그 정의 내에서 자기 자신을 참조한다.
유한한 방법으로 무한 집합 정의란 유한한 설명으로 무한한 요소를 포함하는 집합을 정의할 수 있다. 복잡하고 무한한 패턴과 구조를 간단하고 명확한 규칙으로 표현할 수 있다.
예를 들어, 연결 리스트는 빈 리스트는 연결 리스트이고, 단일 노드 뒤에 연결 리스트가 오면 그것도 연결리스트이다.
이진 트리는 빈 트리는 이진 트리이고 두 개의 자식을 가진 노드가 모두 이진 트리일 경우 그 노드도 이진 트리이다.
귀납적 정의에는 Top-down, Bottom-up, Rules of inference가 있다.
Top-Down
자연수 N의 부분 집합 S의 자연수 n에 대하여,
1) n = 0, 0 ∈ S이다.
2) n이 집합 S에 속한다면 n-3도 속해있다.
위 집합은 자기 자신을 참조하여 정의하기에 귀납적이다. 여기서 S는 어떤 집합인지 Top-Down 방법을 통하여 알아보자.
0은 정의의 첫 번째 조건에 의해 S에 속한다.
3은 3-3 = 0이므로, 또 0이 S에 속하기 때문에 S에 속한다.
6은 6-3 = 3이고 3은 S에 속하기 때문에 S에 속한다.
따라서, {0, 3, 6, 9 ...}이 S에 속한다고 추측할 수 있다.
이를 정리하면,
Base Case: k=0일 때, 3k ∈ S 이다.
Inductive Case: 3k ∈ S라고 가정할 때, 3(k+1) ∈ S를 보여야하는데, 3(k+1)-3 = 3k ∈ S에 속하기에 성립한다.
다른 숫자들은 왜 S에 포함되지 않을까?
1은 1-3 = -2이므로 포함되지 않는다. 마찬가지로 2는 3을 빼면 -1이므로 포함되지 않는다.
4는 4-3은 1이고, 1은 S에 포함되지 않으므로 4 또한 포함되지 않는다.
Bottom-Up
자연수 N의 부분집합 S는 아래 조건을 만족하는 가장 작은 집합이다.
1) 0 ∈ S 이다.
2) n ∈ S라면, n+3 ∈ S이다.
위 두 조건을 충족하는 집합은 {0, 3, 6, 9...}, {1, 4, 7, 10...} 심지어 {0, 3, 6, 9...} ∪ {1, 4, 7, 10...} 도 충족한다.
하지만 S는 그러한 집합 중 가장 작은 집합이므로, {0, 3, 6, 9 ...}로 유일해진다.
Rules of Inference (추론 규칙)
추론 규칙은 다음과 같은 규칙을 가진다.

여기서 A는 가설(전제), B는 결론이다.
만약 A가 참이라면 B도 참이라는 의미를 가진다.
B 단독으로도 공리(가설 없이 사용되는 추론 규칙)가 될 수 있다.
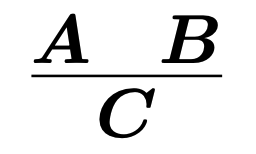
가설은 여러 명제를 포함할 수 있으며, 이는 A와 B가 모두 참이라면 C도 참이라는 의미를 가진다.
앞서 계속 다룬 정의는 추론 규칙에서 아래와 같이 나타낼 수 있다.

먼저 0 ∈ S라는 공리가 존재한다.
여기서 추론 규칙에 따라 n ∈ S이 참이라면 (n+3) ∈ S 도 참이다.
S는 추론 규칙에 따라 닫혀 있는 가장 작은 집합이다.
연습 문제

위 조건을 만족하는 집합을 찾아보자.
3 ∈ S일 때, x ∈ S이고 y ∈ S라면 x+y ∈ S여야 한다.
이러한 조건을 만족하는 집합은 {3, 6, 9, 12, ...}으로, 3의 배수로 이뤄진 집합을 정의한다.

위 조건을 만족하는 집합을 찾아보자.
먼저, "()"은 집합에 속해있다.
또 집합에 요소 x가 있다면 "(x)" 또한 존재한다.
또 x와 y가 있다면 xy도 존재한다.
따라서 위 집합은 {(), (()), ()(), (())(), (())(()), ((())), ...} 이다.

위 집합을 추론 규칙에 따라 정의해보자.
먼저 집합에 a와 b가 존재해야 한다. 따라서 /a, /b 라는 공리가 있다.
그리고 집합에 있는 요소 뒤에는 a 또는 b가 붙을 수 있다. 따라서 위 집합의 추론 규칙은,
/{a, b} ⊂ S, x ∈ S/xa ∈ S, x ∈ S/xb ∈ S 이다.

위 집합을 추론 규칙에 따라 정의해보자.
n ∈ N이므로, n은 0 이상의 모든 정수이다.
n = 0일 때, b이다. n = 1 일 때, abb이다.
따라서 위 집합의 추론 규칙은,
/b ∈ S, x ∈ S / axb 이다.
'학교강의필기장 > 프로그래밍언어론' 카테고리의 다른 글
| 6. 간단한 언어 만들어보기 - 2 (1) | 2024.04.21 |
|---|---|
| 5. 간단한 언어 만들어보기 - 1 (1) | 2024.04.21 |
| 4. OCaml - 재귀, 꼬리재귀와 고차함수 (0) | 2024.04.21 |
| 3. OCaml - 개요, 타입 및 연산, 패턴, 리스트, 튜플, 사용자정의타입, 예외처리 (0) | 2024.04.21 |
| 2. 귀납적 정의 (Inductive Definitions) 2 (0) | 2024.04.16 |
